题目内容
13．i为虚数单位，复数（1+i）2+$\frac{2}{1-i}$的共轭复数是（ ）| A． | 1+3i | B． | -1+3i | C． | 1-3i | D． | -1-3i |
分析 直接利用复数代数形式的乘除运算化简求得z，再由共轭复数的概念得答案．
解答 解：∵（1+i）2+$\frac{2}{1-i}$=$2i+\frac{2（1+i）}{（1-i）（1+i）}=2i+1+i=1+3i$，
∴$\overline{z}=1-3i$．
故选：C．
点评 本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础的计算题．
练习册系列答案
相关题目
3．直角坐标系中，点$（1，-\sqrt{3}）$的极坐标可以是（ ）
| A． | $（2，\frac{5π}{6}）$ | B． | $（2，\frac{11π}{6}）$ | C． | $（2，\frac{4π}{3}）$ | D． | $（2，\frac{5π}{3}）$ |
4．一几何体由一个四棱锥和一个球组成，四棱锥的顶点都在球上，几何体的三视图如图所示，其中正视图和侧视图完全相同，球的表面积是36π，四棱锥的体积为（ ）
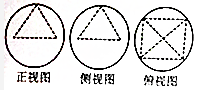
| A． | 18 | B． | 9 | C． | 9$\sqrt{2}$ | D． | 18$\sqrt{2}$ |
1．已知复数z1=2t+i，z2=1-2i，若$\frac{z_1}{z_2}$为实数，则实数t的值是（ ）
| A． | 1 | B． | -1 | C． | $\frac{1}{4}$ | D． | -$\frac{1}{4}$ |
8．若3a2+3b2-4c2=0，则直线ax+by+c=0被圆x2+y2=1所截得的弦长为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | 1 |
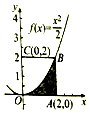如图，利用随机模拟的方法可以估计图中由曲线$y=\frac{x^2}{2}$与两直线x=2及y=0所围成的阴影部分的面积S：