Question

实数集上的奇函数f（x）为增函数，偶函数g（x）在非负数集上的图象与f（x）的图象重合，设a＞b＞0，下列不等式中成立的是

 

．
（1）f（b）-f（-a）＞g（a）-g（-b） 　　（2）f（b）-f（-a）＜g（a）-g（-b）
（3）f（a）-f（-b）＞g（b）-g（-a） 　　（4）f（a）-f（-b）＜g（b）-g（-a）

Answer 1

考点：奇偶性与单调性的综合

专题：函数的性质及应用

分析：根据题意画出满足条件的函数图象，再由函数的奇偶性得：f（-a）=-f（a），f（-b）=-f（b），g（-a）=g（a）=f（a），g（-b）=g（b）=f（b），结合图象对选项中的不等式进行转化验证即可．

解答： 解：f（x）在（-∞，+∞）上为奇函数，且为增函数，g（x）为偶函数且在[0，+∞）上图象与f（x）重合，
且a＞b＞0，可画图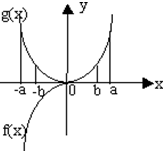如下：
由图得，f（a）＞f（b）＞0
又∵f（-a）=-f（a），f（-b）=-f（b），g（-a）=g（a）=f（a），g（-b）=g（b）=f（b）；
∴f（b）-f（-a）＞g（a）-g（-b）?f（b）+f（a）＞f（a）-f（b）?f（b）＞-f（b），
故（1）对、（2）不对．
f（a）-f（-b）＞g（b）-g（-a）?f（b）+f（a）＞f（b）-f（a）?f（a）＞-f（a），
故（3）对、（4）不对．
故答案为：（1）与（3）．

点评：本题主要考查函数奇偶性的关系式、图象特征的应用，以及数形结合思想，属于中档题．