Question

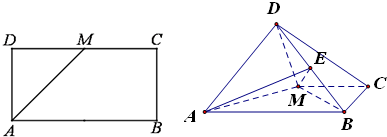
如图，已知长方形ABCD中，AB=2，AD=1，M为CD的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．
（1）求证：AD⊥BM；
（2）若点E是线段BD的中点，求二面角E-AM-D的余弦值．

Answer 1

考点：二面角的平面角及求法

专题：空间角

分析：（1）由已知条件推导出AM⊥BM，BM⊥平面ADM，由此能证明AD⊥BM．
（2）取DM的中点F，则EF∥BM，过F作FH⊥AM，连接EH，由已知条件推导出∠FHE即二面角E-AM-D的平面角，由此能求出二面角E-AM-D的余弦值．

解答： （1）证明：∵AM=BM=

2

，∴AB²=AM²+BM²，即AM⊥BM．
∵平面ADM⊥平面ABCD，∴BM⊥平面ADM，∴AD⊥BM．…（5分）
（2）解：取DM的中点F，则EF∥BM，
由（1）知BM⊥平面ADM，∴EF⊥平面ADM．
过F作FH⊥AM，连接EH，
则∠FHE即二面角E-AM-D的平面角，
由已知EF=

2

2

，FH=

2

4

，
∴EH=

10

4

，∴cos∠FHE=

FH

EH

=

5

5

．
∴二面角E-AM-D的余弦值是

5

5

．…（13分）

点评：本题考查异面直线垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．