题目内容
某种产品的广告费用x与销售额y的统计数据如下表:
(1)利用所给数据求广告费用x与销售额y之间的线性回归方程y=a+bx;
(2)预计在今后的销售中,销售额与广告费用还服从(1)中的关系,如果广告费用为6万元,请预测销售额为多少万元?
附:其中b=
,a=
-b
.
| 广告费用x(万元) | 1 | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 10 | 12 | 15 | 18 | 20 |
(2)预计在今后的销售中,销售额与广告费用还服从(1)中的关系,如果广告费用为6万元,请预测销售额为多少万元?
附:其中b=
x1y1+x2y2+…+xnyn-n
| ||||
x12+x22+…+xn2-n(
|
. |
| y |
. |
| x |
考点:线性回归方程
专题:计算题,概率与统计
分析:(1)利用公式计算回归直线方程的系数,可得回归直线方程;
(2)代入x=6计算y的值,可得预报销售额.
(2)代入x=6计算y的值,可得预报销售额.
解答:
解:(1)
=
,
=
=15;
∴b=2.6,a=7.2,
则广告费用x与销售额y之间的线性回归方程y=2.6x+7.2,
(2)当广告费用为6万元时,由上线性回归方程预测销售额为2.6×6+7.2=22.8万元.
. |
| x |
| 1+2+3+4+5 |
| 5 |
. |
| y |
| 10+12+15+18+20 |
| 5 |
∴b=2.6,a=7.2,
则广告费用x与销售额y之间的线性回归方程y=2.6x+7.2,
(2)当广告费用为6万元时,由上线性回归方程预测销售额为2.6×6+7.2=22.8万元.
点评:本题考查了线性回归方程的求法及利用回归直线方程计算预报变量,熟练掌握最小二乘法求回归系数是解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
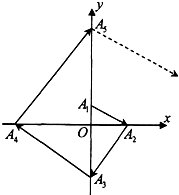 如图所示,点列{An}满足:|
如图所示,点列{An}满足:|| OA1 |
| OAi+1 |
| OAi |
| OA1 |
| OA2 |
| OA2014 |
| A、(22014-1,0) | ||||
| B、(22016-1,22015-1) | ||||
C、(
| ||||
D、(
|
已知函数f(x)=loga(2x+b-1)(a>0且a≠1)的部分图象如图所示,则满足a,b关系是( )
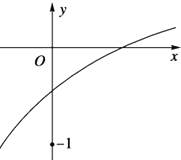

A、0<
| ||||
B、0<b<
| ||||
C、0<
| ||||
D、0<
|