题目内容
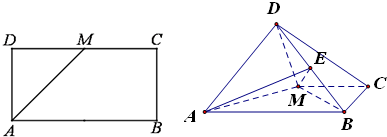
用红、黄、绿、蓝四种不同颜色给一个正方体的六个面涂色,要求相邻两个面涂不同的颜色,则共有涂色方法(涂色后,任意翻转正方体,能使正方体各面颜色一致,我们认为是同一种涂色方法)( )
| A、10种 | B、12种 |
| C、24种 | D、48种 |
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:由于涂色过程中,要保证满足用四种颜色,且相邻的面不同色,对于正方体的三对面来说,必然有三对同色或两对同色,一对不同色,而且三对面具有“地位对等性”.
解答:
解:由于涂色过程中,要保证满足用四种颜色,且相邻的面不同色,对于正方体的三对面来说,必然有三对同色或两对同色,一对不同色,而且三对面具有“地位对等性”,因此,
三对同色:
=4种不同的涂法;
两对同色,一对不同色:只需从四种颜色中选择2种涂在其中两对面上,剩下的两种颜色涂在另外两个面即可.因此共有
=6种不同的涂法.
故共有4+6=10种不同的涂法.
故选:A.
三对同色:
| C | 3 4 |
两对同色,一对不同色:只需从四种颜色中选择2种涂在其中两对面上,剩下的两种颜色涂在另外两个面即可.因此共有
| C | 2 4 |
故共有4+6=10种不同的涂法.
故选:A.
点评:本题考查了排列,组合和简单的计数问题,解答该题的关键是对题目中注明的涂色后,任意翻转正方体,能使正方体各面颜色一致,我们认为是同一种涂色方法的理解,这样使看似复杂的问题变为简单的选色(即组合)问题,属中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
已知全集U=R,集合A={x|
<0|,B={x|lgx≥0},则集合{x|x≤1}等于( )
| x |
| 1-x |
| A、A∩B |
| B、A∪B |
| C、∁U(A∩B) |
| D、∁U(A∩B) |
已知i为复数单位,若
=1+bi(a,b∈R),则a+b=( )
| 1+ai |
| i |
| A、2 | B、1 | C、-1 | D、0 |
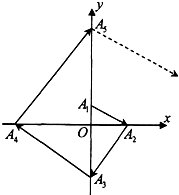 如图所示,点列{An}满足:|
如图所示,点列{An}满足:|| OA1 |
| OAi+1 |
| OAi |
| OA1 |
| OA2 |
| OA2014 |
| A、(22014-1,0) | ||||
| B、(22016-1,22015-1) | ||||
C、(
| ||||
D、(
|
若函数f(x)=
+
是奇函数,则a的值为( )
| 1 |
| 3x-1 |
| 1 |
| a |
| A、1 | B、2 | C、3 | D、4 |
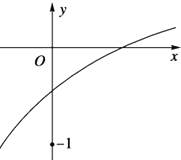
已知函数f(x)=loga(2x+b-1)(a>0且a≠1)的部分图象如图所示,则满足a,b关系是( )

A、0<
| ||||
B、0<b<
| ||||
C、0<
| ||||
D、0<
|