题目内容
已知函数f(x)=ax-1-lnx(a∈R).
(1)当a=1时,求曲线在点(1,0)处的切线方程;
(2)求函数f(x)在区间[
,2]上的最小值;
(3)证明不等式:2•
•
…
<e
.
(1)当a=1时,求曲线在点(1,0)处的切线方程;
(2)求函数f(x)在区间[
| 1 |
| 2 |
(3)证明不等式:2•
| 4 |
| 3 |
| 8 |
| 7 |
| 2n |
| 2n-1 |
| 5 |
| 3 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)利用导数与曲线斜率的公式即可求得结论;
(2)分类讨论,利用导数即可求得函数的最小值;
(3)利用(1)的结论得lnx≤x-1,故ln[(1+1)(1+
)(1+
)…(1+
)]=ln(1+1)+ln(1+
)+ln(1+
)…+ln(1+
)≤1+
+…+
利用不等式放缩即可得出结论.
(2)分类讨论,利用导数即可求得函数的最小值;
(3)利用(1)的结论得lnx≤x-1,故ln[(1+1)(1+
| 1 |
| 3 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 3 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
利用不等式放缩即可得出结论.
解答:
解:(1)函数f(x)的定义域为(0,+∞)
当a=1时,f′(x)=1-
,则f'(1)=0,故曲线在点(1,0)处的切线为y=0.
(2)f′(x)=
(x>0),则
①当a≤0时,f'(x)<0,
此时f(x)在[
,2]上单减,故f(x)min=f(2)=2a-1-ln2
②当a>0时,
(Ⅰ)0<
≤
,即a≥2,f(x)在上单增,故f(x)min=f(
)=
-1+ln2;
(Ⅱ)
<
<2,即
<a<2,f(x)在[
,
)单减,在[
,2]单增,故f(x)min=f(
)=lna.
(Ⅲ)
≥2,即0<a≤
,f(x)在[
,2]上单减,故f(x)min=f(2)=2a-1-ln2
综上f(x)min=
(3)由(1)知,当a=1时,f(x)在(0,1)上单调递减;在(1,+∞)上单调递增.则函数f(x)在x=1处取得极小值,也即在区间(0,+∞)的最小值.
则∵f(x)=x-1-lnx≥f(1)=0,
∴lnx≤x-1
故当n∈N*且n≥2时,ln[(1+1)(1+
)(1+
)…(1+
)]=ln(1+1)+ln(1+
)+ln(1+
)…+ln(1+
)≤1+
+…+
∵
=
<
=2(
-
)
∴1+
+…+
<1+2[(
-
)+…+(
-
)]
∴ln(1+1)+ln(1+
)+ln(1+
)…+ln(1+
)<
即(1+1)(1+
)(1+
)…(1+
)<e
.
当a=1时,f′(x)=1-
| 1 |
| x |
(2)f′(x)=
| ax-1 |
| x |
①当a≤0时,f'(x)<0,
此时f(x)在[
| 1 |
| 2 |
②当a>0时,
(Ⅰ)0<
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
(Ⅱ)
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
(Ⅲ)
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
综上f(x)min=
|
(3)由(1)知,当a=1时,f(x)在(0,1)上单调递减;在(1,+∞)上单调递增.则函数f(x)在x=1处取得极小值,也即在区间(0,+∞)的最小值.
则∵f(x)=x-1-lnx≥f(1)=0,
∴lnx≤x-1
故当n∈N*且n≥2时,ln[(1+1)(1+
| 1 |
| 3 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 3 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
∵
| 1 |
| 2n-1 |
| 2n+1-1 |
| (2n-1)(2n+1-1) |
| 2n+1 |
| (2n-1)(2n+1-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
∴1+
| 1 |
| 3 |
| 1 |
| 2n-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1-1 |
∴ln(1+1)+ln(1+
| 1 |
| 3 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 5 |
| 3 |
即(1+1)(1+
| 1 |
| 3 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 5 |
| 3 |
点评:本题主要考查利用导数研究曲线的切线方程及判断函数的单调性求函数的最值等知识,考查学生分析问题解决问题的能力,考查学生的运算求解能力及分类讨论思想转化划归思想的运用能力,综合性、逻辑性强,属难题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
已知△ABC中,|
|=2,A=
,则|
+
|有( )
| BC |
| π |
| 3 |
| AB |
| AC |
A、最大值
| ||
B、最大值2
| ||
C、最小值
| ||
D、最小值2
|
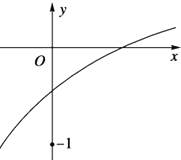
已知函数f(x)=loga(2x+b-1)(a>0且a≠1)的部分图象如图所示,则满足a,b关系是( )

A、0<
| ||||
B、0<b<
| ||||
C、0<
| ||||
D、0<
|