题目内容
已知tanθ=2,则
=( )
2sin2(θ-
| ||
| 1+cos2θ |
A、
| ||
| B、1 | ||
C、
| ||
D、-
|
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:计算题
分析:原式利用诱导公式化简,再利用同角三角函数间的基本关系变形,将tanθ的值代入计算即可求出值.
解答:
解:∵tanθ=2,
∴原式=
=
=
=
=
=-
.
故选:D.
∴原式=
1-cos(2θ-
| ||
1+
|
| 2-2sin2θ+2cos2θ |
| 3+cos2θ |
| 4cos2θ-4sinθcosθ |
| 4cos2θ+2sin2θ |
| 4-4tanθ |
| 4+2tan2θ |
| 4-8 |
| 4+8 |
| 1 |
| 3 |
故选:D.
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
已知全集U=R,集合A={x|
<0|,B={x|lgx≥0},则集合{x|x≤1}等于( )
| x |
| 1-x |
| A、A∩B |
| B、A∪B |
| C、∁U(A∩B) |
| D、∁U(A∩B) |
已知命题p:?x∈R,lnx+x-2=0,命题q:?x∈R,2x≥x2,则下列命题中为真命题的是( )
| A、p∧q | B、¬p∧q |
| C、p∧¬q | D、¬p∧¬q |
已知△ABC中,|
|=2,A=
,则|
+
|有( )
| BC |
| π |
| 3 |
| AB |
| AC |
A、最大值
| ||
B、最大值2
| ||
C、最小值
| ||
D、最小值2
|
已知i为复数单位,若
=1+bi(a,b∈R),则a+b=( )
| 1+ai |
| i |
| A、2 | B、1 | C、-1 | D、0 |
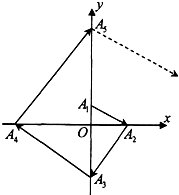 如图所示,点列{An}满足:|
如图所示,点列{An}满足:|| OA1 |
| OAi+1 |
| OAi |
| OA1 |
| OA2 |
| OA2014 |
| A、(22014-1,0) | ||||
| B、(22016-1,22015-1) | ||||
C、(
| ||||
D、(
|
 如图,设G、H分别为△ABC的重心、垂心,F为线段GH的中点,若△ABC外接圆的半径为1,则|
如图,设G、H分别为△ABC的重心、垂心,F为线段GH的中点,若△ABC外接圆的半径为1,则|