题目内容
已知定义域为R的函数f(x)=
是奇函数
①求a、b的值;
②证明f(x)在R上是减函数.
| -2x+b |
| 2x+1+a |
①求a、b的值;
②证明f(x)在R上是减函数.
考点:函数奇偶性的性质,函数单调性的判断与证明
专题:函数的性质及应用
分析:①根据定义域为R的函数f(x)=
是奇函数,可得f(0)=0,f(-1)=-f(1),解出即可;
②利用减函数的定义即可证明.
| -2x+b |
| 2x+1+a |
②利用减函数的定义即可证明.
解答:
①解:∵定义域为R的函数f(x)=
是奇函数,
∴f(0)=0,f(-1)=-f(1),
∴
=0,
=-
,
解得b=1,a=2.
②证明:由①可得:f(x)=
=
-
.
?x1<x2,∴2x2>2x1>0,
则f(x1)-f(x2)=
-
-(
-
)=
>0,
∴f(x1)>f(x2).
∴f(x)在R上是减函数.
| -2x+b |
| 2x+1+a |
∴f(0)=0,f(-1)=-f(1),
∴
| -1+b |
| 2+a |
| -2-1+b |
| 1+a |
| -2+b |
| 4+a |
解得b=1,a=2.
②证明:由①可得:f(x)=
| -2x+1 |
| 2x+1+2 |
| 1 |
| 2x+1 |
| 1 |
| 2 |
?x1<x2,∴2x2>2x1>0,
则f(x1)-f(x2)=
| 1 |
| 2x1+1 |
| 1 |
| 2 |
| 1 |
| 2x2+1 |
| 1 |
| 2 |
| 2x2-2x1 |
| (2x1+1)(2x2+1) |
∴f(x1)>f(x2).
∴f(x)在R上是减函数.
点评:本题考查了函数的奇偶性、单调性,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
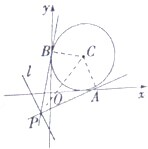 已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.
已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.