题目内容
圆锥的侧面面积是底面面积的2倍,则圆锥的母线与底面所成的角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:旋转体(圆柱、圆锥、圆台)
专题:计算题
分析:由圆锥的侧面积是其底面积的2倍,我们易求出圆锥的母线与底面半径之间的关系,解由圆锥高、底面半径、圆锥母线构成的直角三角形,即可求出圆锥的母线与底面所成的角.
解答:
解:设圆锥的底面半径为R,母线长为l,则:
其底面积:S底面积=πR2,
其侧面积:S侧面积=
•2πR•l=πRl
∵圆锥的侧面积是其底面积的2倍,
∴πRl=2πR2,即l=2R,
故该圆锥的母线与底面所成的角θ满足:cosθ=
=
,
∴θ=
.
故选A.
其底面积:S底面积=πR2,
其侧面积:S侧面积=
| 1 |
| 2 |
∵圆锥的侧面积是其底面积的2倍,
∴πRl=2πR2,即l=2R,
故该圆锥的母线与底面所成的角θ满足:cosθ=
| R |
| l |
| 1 |
| 2 |
∴θ=
| π |
| 3 |
故选A.
点评:本题考查的知识点是旋转体的性质,根据圆锥的侧面积是其底面积的2倍,求出圆锥的母线与底面半径之间的关系是解答本题的关键,属于基础题.

练习册系列答案
相关题目
若集合M={x|x2+x-6=0},N={x|ax-1=0},且M∩N=N,则实数a的取值组成的集合是 ( )
A、{
| ||||
B、{-
| ||||
C、{-
| ||||
D、{-
|
当
<x<
时,函数f(x)=
的最小值是( )
| π |
| 4 |
| π |
| 2 |
| sin2x |
| 2cosx(sinx-cosx) |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
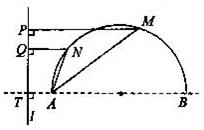 如图,已知半圆的直径|AB|=20,l为半圆外一直线,且与BA的延长线交于点T,|AT|=4,半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件
如图,已知半圆的直径|AB|=20,l为半圆外一直线,且与BA的延长线交于点T,|AT|=4,半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件| |MP| |
| |MA| |
| |NQ| |
| |NA| |
| A、22 | B、20 | C、18 | D、16 |
若
=b,则a+b=( )
| lim |
| x→1 |
| x+a | |||
|
| A、-2 | B、0 | C、2 | D、4 |