题目内容
两人轮流掷骰子,每人每次投掷两颗,第一个使两颗骰子点数和大于6者为胜,否则,由另一个人投掷,则先投掷人获胜的概率是 .
考点:等可能事件的概率,等比数列的前n项和
专题:计算题
分析:根据题意,首先由等可能事件的概率公式计算每次抛掷两颗骰子点数和大于6的概率,由对立事件的概率性质,可得点数和小于等于6的概率;分别求出先投掷的人第一轮获胜、第二轮获胜…的概率,分析可得P1、P2、P3、…Pn、…,组成以
首项,(
)2为公比的无穷等比数列,由等比数列的前n项和公式,结合极限计算方法,计算可得答案.
| 7 |
| 12 |
| 5 |
| 12 |
解答:
解:根据题意,一次投掷两颗,每颗骰子有6种情况,共有6×6=36种情况,
而点数之和大于6的情况有21种,则每次抛掷两颗骰子点数和大于6的概率为
=
,
则抛掷每次两颗骰子点数和小于等于6的概率为1-
=
;
若先投掷的人第一轮获胜,其概率为P1=
,
若先投掷的人第二轮获胜,即第一轮两人的点数之和都小于或等于6,则其概率为P2=(
)2×
,
若先投掷的人第三轮获胜,即前两轮两人的点数之和都小于或等于6,则其概率为P3=(
)4×
,
若先投掷的人第四轮获胜,即前三轮两人的点数之和都小于或等于6,则其概率为P3=(
)6×
,
…
分析可得,若先投掷的人第n轮获胜,其概率为Pn=(
)2n-2×
,
P1、P2、P3、…Pn、…,组成以
首项,(
)2为公比的无穷等比数列,
则先投掷的人获胜的概率P1+P2+P3+…+Pn+…=
,
又由极限的性质,可得P1+P2+P3+…+Pn+…=
=
;
故答案为
.
而点数之和大于6的情况有21种,则每次抛掷两颗骰子点数和大于6的概率为
| 21 |
| 36 |
| 7 |
| 12 |
则抛掷每次两颗骰子点数和小于等于6的概率为1-
| 7 |
| 12 |
| 5 |
| 12 |
若先投掷的人第一轮获胜,其概率为P1=
| 7 |
| 12 |
若先投掷的人第二轮获胜,即第一轮两人的点数之和都小于或等于6,则其概率为P2=(
| 5 |
| 12 |
| 7 |
| 12 |
若先投掷的人第三轮获胜,即前两轮两人的点数之和都小于或等于6,则其概率为P3=(
| 5 |
| 12 |
| 7 |
| 12 |
若先投掷的人第四轮获胜,即前三轮两人的点数之和都小于或等于6,则其概率为P3=(
| 5 |
| 12 |
| 7 |
| 12 |
…
分析可得,若先投掷的人第n轮获胜,其概率为Pn=(
| 5 |
| 12 |
| 7 |
| 12 |
P1、P2、P3、…Pn、…,组成以
| 7 |
| 12 |
| 5 |
| 12 |
则先投掷的人获胜的概率P1+P2+P3+…+Pn+…=
| ||||
1-(
|
又由极限的性质,可得P1+P2+P3+…+Pn+…=
| ||
1-(
|
| 12 |
| 17 |
故答案为
| 12 |
| 17 |
点评:本题考查等可能事件的概率的计算,涉及等比数列的前n项和与极限的计算;关键是分类分析、计算先投掷的人获胜的情况,进而由等比数列前n项公式计算.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
下表是X的分布列,则a=( )
| X | 1 | 2 | 3 |
| P | 0.5 | a | 0.3 |
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
圆锥的侧面面积是底面面积的2倍,则圆锥的母线与底面所成的角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
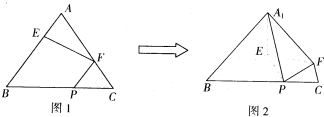 如图1,在正三角形ABC中,已知AB=5,E、F、P分别是AB、AC、BC边上的点,设
如图1,在正三角形ABC中,已知AB=5,E、F、P分别是AB、AC、BC边上的点,设
 设图中的正方体的棱长为a(1)图中哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小.(3)求异面直线BC和AA1的距离.
设图中的正方体的棱长为a(1)图中哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和CC1所成的角的大小.(3)求异面直线BC和AA1的距离.