题目内容
当0＜a＜1时，函数y=ax 和y=（a-1）x2的图象只能是下图中的（ ）
A、 |
B、 |
C、 |
D、 |
考点：指数函数的图像变换
专题：函数的性质及应用
分析：当0＜a＜1时，函数y=ax 是指数函数，且在定义域上是减函数；而函数y=（a-1）x2 的图象是开口向下的抛物线，结合所给的选项，可得结论．
解答：
解：当0＜a＜1时，函数y=ax 是指数函数，且在定义域上是减函数；
而函数y=（a-1）x2 是二次函数，它的图象是开口向下的抛物线，
故选：D．
而函数y=（a-1）x2 是二次函数，它的图象是开口向下的抛物线，
故选：D．
点评：本题主要指数函数、二次函数的图象特征，属于基础题．
练习册系列答案
相关题目
极坐标方程ρ=cosθ化为直角坐标方程为（ ）
A、（x+
| ||||
B、x2+（y+
| ||||
C、x2+（y-
| ||||
D、（x-
|
a，b，c，d均为实数，下列命题正确的个数有（ ）
①a＞b，c＞b⇒a＞c；②a＞-b⇒c-a＜c+b；③a＞b⇒ac2＞bc2； ④a＞b，c＞d⇒ac＞bd；⑤
＞
⇒a＞b．
①a＞b，c＞b⇒a＞c；②a＞-b⇒c-a＜c+b；③a＞b⇒ac2＞bc2； ④a＞b，c＞d⇒ac＞bd；⑤
| a |
| c2 |
| b |
| c2 |
| A、1 | B、2 | C、3 | D、4 |
以下命题不正确的是（ ）
| A、?x∈N，lgx=2 | ||||
B、双曲线
| ||||
| C、?x∈R，2x-1＞0 | ||||
D、抛物线x=2y2的准线方程为x=-
|
已知函数f（x）=
，则（ ）
| x2 |
| x-1 |
| A、f（x）有极大值4 |
| B、f（x）有极小值0 |
| C、f（x）有极小值-4 |
| D、f（x）有极大值0 |
点（
，0）到直线x-y=0的距离为（ ）
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
函数y=
的定义域是（ ）
| lg(2-x) | ||
|
| A、（1，2） |
| B、[1，2） |
| C、[1，+∞） |
| D、（-∞，2） |
函数F（x）=
t（t-4）dt在[-1，5]上（ ）
| ∫ | x 0 |
| A、有最大值0，无最小值 | ||
B、有最大值0，最小值-
| ||
C、有最小值-
| ||
| D、既无最大值也无最小值 |
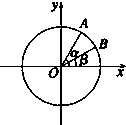如图，在平面直角坐标系xOy中，以OX轴的非负半轴为始边作两个锐角α、β，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为