��Ŀ����
16��ijѧУΪ���ƶ�����ѧУ�ſ���ѧ�������ڼ�ҳ����ͺ�����ͣ������Ĵ�ʩ����ȫУѧ���ҳ��������ʾ����飮���ݴ����������ȡ��50�ݵ����ʾ����õ������µ���������| ͬ��������ͣ�� | ��ͬ��������ͣ�� | �ϼ� | |
| �� | 18 | 7 | 25 |
| Ů | 12 | 13 | 25 |
| �ϼ� | 30 | 20 | 50 |
������֪��ͬ��������ͣ����12λŮ�Լҳ��У���3λ�ճ��������ͺ��ӣ��ִ���12λŮ�Լҳ��������ȡ3�˲���ά�����Dz���ά�������Ů�Լҳ��У��ճ��������ͺ��ӵ�Ů�Լҳ�����Ϊ�Σ���εķֲ��к���ѧ������
���� ����������֪����������ԡ�Ů��ѡ��$\frac{5}{30}��12=2$�ˣ�Ȼ����������һ��Ů�Եĸ��ʣ�
���������������ε����п���ȡֵΪ0��1��2��3��������ʣ��õ��ֲ��У�Ȼ�����������
��� �⣺����������֪������ѡ��$\frac{5}{30}��18=3$�ˣ�
Ů��ѡ��$\frac{5}{30}��12=2$�ˣ���5�˲���ά������
����ѡ��2�˵����м��ˣ���������һ��Ů�Եĸ���Ϊ$P=\frac{C_2^1C_3^1+C_2^2}{C_5^2}=\frac{7}{10}$��
����������֪��ͬ��������ͣ����12λŮ�Լҳ��У�ѡ������ά�������Ů�Լҳ�����Ϊ3�ˣ�
��������ε����п���ȡֵΪ0��1��2��3��
����$P����=0��=\frac{C_9^3}{{C_{12}^3}}=\frac{21}{55}$��$P����=1��=\frac{C_9^2C_3^1}{{C_{12}^3}}=\frac{27}{55}$��$P����=2��=\frac{C_9^1C_3^2}{{C_{12}^3}}=\frac{27}{220}$��$P����=3��=\frac{C_3^3}{{C_{12}^3}}=\frac{1}{220}$��
��˦εķֲ���Ϊ
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{21}{55}$ | $\frac{27}{55}$ | $\frac{27}{220}$ | $\frac{1}{220}$ |
���� ���⿼����ʵ�Ӧ�ã��ֲ����Լ���������������������������������

��ϰ��ϵ�д�
�����Ŀ
7���ڡ�ABC����ƽ������һ��P������$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{BC}$��$\overrightarrow{PC}=x\overrightarrow{AB}+y\overrightarrow{AC}$����x+y=��������
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $-\frac{1}{3}$ | D�� | $-\frac{1}{2}$ |
11������P��1��-3����ֱ����������y=x2���У�����Բ��x-2��2+y2=5���У������ߵ�б��Ϊ��������
| A�� | -6 | B�� | -2 | C�� | -1 | D�� | 3 |
1����֪����A={0��2��4}��B={x|3x-x2��0}����A��B���Ӽ�����Ϊ��������
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 8 |
5��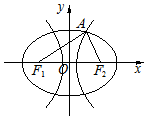 ��ͼ����Բ��˫�����й�������F1��F2�������ڵ�һ���Ľ���ΪA����AF1��AF2
��ͼ����Բ��˫�����й�������F1��F2�������ڵ�һ���Ľ���ΪA����AF1��AF2
��AF1F2=30�㣬����Բ��˫���ߵ������ʵ�֮��Ϊ��������
 ��ͼ����Բ��˫�����й�������F1��F2�������ڵ�һ���Ľ���ΪA����AF1��AF2
��ͼ����Բ��˫�����й�������F1��F2�������ڵ�һ���Ľ���ΪA����AF1��AF2��AF1F2=30�㣬����Բ��˫���ߵ������ʵ�֮��Ϊ��������
| A�� | 2 | B�� | $\sqrt{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{\sqrt{3}}{2}$ |
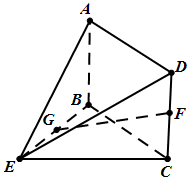 ��ͼ���ڼ�����ABCDE�У��ı���ABCD�Ǿ��Σ�AB��ƽ��BCE��BE��CE��AB=BE=EC=2��G��F�ֱ����߶�BE��DC���е㣮
��ͼ���ڼ�����ABCDE�У��ı���ABCD�Ǿ��Σ�AB��ƽ��BCE��BE��CE��AB=BE=EC=2��G��F�ֱ����߶�BE��DC���е㣮 18���ס�����λͬѧ�μ���ѧ�Ļ�֪ʶ������ѵ���ֱַ����������ѵ�ڼ�μӵ����ɴβ��Գɼ��������ȡ8�Σ���¼���£�
18���ס�����λͬѧ�μ���ѧ�Ļ�֪ʶ������ѵ���ֱַ����������ѵ�ڼ�μӵ����ɴβ��Գɼ��������ȡ8�Σ���¼���£�