题目内容
4.若函数f(x)满足:集合A={f(n)|n∈N*}中至少存在三个不同的数构成等差数列,则称函数f(x)是等差源函数.判断下列函数:①y=log2x;
②y=2x;
③y=$\frac{1}{x}$中,
所有的等差源函数的序号是( )
| A. | ① | B. | ①② | C. | ②③ | D. | ①③ |
分析 利用等差源函数的定义、等差数列的定义即可判断出结论.
解答 解:①∵log21,log22,log24构成等差数列,∴y=log2x是等差源函数;
②y=2x不是等差源函数,因为若是,则2×2p=2m+2n,则2p+1=2m+2n,
∴2p+1-n=2m-n+1,左边是偶数,右边是奇数,故y=2x+1不是等差源函数;
③取$\frac{1}{2},\frac{1}{3},\frac{1}{6}$成等差数列,因此y=$\frac{1}{x}$是等差源函数.
综上可得:只有①③正确.
故选:D.
点评 本题考查了等差源函数的定义、等差数列的定义,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
19.下列四个函数中,在其定义域上既是奇函数又是单调递增函数的是( )
| A. | y=ex | B. | y=sinx | C. | $y=\sqrt{x}$ | D. | y=x3 |
16.已知直线3x+(1-a)y+1=0与直线x-y+2=0平行,则a的值为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
13.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( )
| A. | $y={(\frac{1}{2})^x}$ | B. | y=-x2 | C. | y=log2x | D. | y=|x|+1 |
14.某四棱锥的三视图如图所示,该四棱锥的四个侧面的面积中最大的是( )
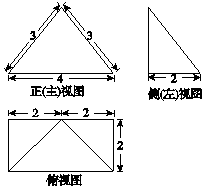

| A. | 3 | B. | $2\sqrt{5}$ | C. | 6 | D. | $3\sqrt{5}$ |
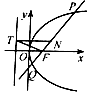 如图所示,抛物线C:y2=2px(p>0)的焦点为F,经过点F的直线l与抛物线交于P,Q两点,弦PQ的中点为N,经过点N作y轴的垂线与C的准线交于点T.
如图所示,抛物线C:y2=2px(p>0)的焦点为F,经过点F的直线l与抛物线交于P,Q两点,弦PQ的中点为N,经过点N作y轴的垂线与C的准线交于点T.