题目内容
13．下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（ ）| A． | $y={（\frac{1}{2}）^x}$ | B． | y=-x2 | C． | y=log2x | D． | y=|x|+1 |
分析 根据函数奇偶性和单调性的性质进行判断即可．
解答 解：A.$y={（\frac{1}{2}）^x}$是减函数，为非奇非偶函数，不满足条件．
B．y=-x2是偶函数，在区间（0，+∞）上单调递减，不满足条件．
C．y=log2x在区间（0，+∞）上单调递增，为非奇非偶函数，不满足条件．
D．y=|x|+1是偶函数又在区间（0，+∞）上单调递增，满足条件．
故选：D
点评 本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．
练习册系列答案
相关题目
3．已知集合A={-3，-2，-1，0，1，2}，B={x|x2≤3}，则A∩B=．（ ）
| A． | {0，2} | B． | {-1，0，1} | C． | {-3，-2，-1，0，1，2} | D． | [0，2] |
4．若函数f（x）满足：集合A={f（n）|n∈N*}中至少存在三个不同的数构成等差数列，则称函数f（x）是等差源函数．判断下列函数：
①y=log2x；
②y=2x；
③y=$\frac{1}{x}$中，
所有的等差源函数的序号是（ ）
①y=log2x；
②y=2x；
③y=$\frac{1}{x}$中，
所有的等差源函数的序号是（ ）
| A． | ① | B． | ①② | C． | ②③ | D． | ①③ |
1．甲袋中有16个白球和17个黑球，乙袋中有31个白球，现每次任意从甲袋中摸出两个球，如果两球同色，则将这两球放进丙袋，并从乙袋中拿出一白球放回甲袋；如果两球不同色，则将白球放进丙袋，并把黑球放回甲袋．那么这样拿 次后，甲袋中只剩一个球，这个球的颜色是 （ ）
| A． | 16，黑色 | B． | 16，白色或黑色 | C． | 32，黑色 | D． | 32，白色 |
8．昌平区在滨河公园举办中学生冬季越野赛．按年龄段将参赛学生分为A，B，C三个组，各组人数如下表所示．组委会用分层抽样的方法从三个组中选出6名代表．
（ I） 求A，B，C三个组各选出代表的个数；
（ II） 若从选出的6名代表中随机抽出2人在越野赛闭幕式上发言，求这两人来自同一组的概率P1；
（ III）若从所有参赛的300名学生中随机抽取2人在越野赛闭幕式上发言，设这两人来自同一组的概率为P2，试判断P1与P2的大小关系（不要求证明）．
| 组别 | A | B | C |
| 人数 | 100 | 150 | 50 |
（ II） 若从选出的6名代表中随机抽出2人在越野赛闭幕式上发言，求这两人来自同一组的概率P1；
（ III）若从所有参赛的300名学生中随机抽取2人在越野赛闭幕式上发言，设这两人来自同一组的概率为P2，试判断P1与P2的大小关系（不要求证明）．
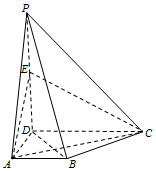如图，在四棱锥P-ABCD 中，PD⊥底面ABCD，AB∥DC，CD=2AB，AD⊥CD，E为棱PD的中点．