题目内容
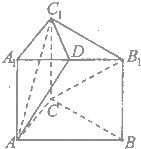 如图在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=CC1=6,BC=8,AB=10,点D是A1B1的中点.
如图在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=CC1=6,BC=8,AB=10,点D是A1B1的中点.(Ⅰ)求证:BC⊥AC1;
(Ⅱ)求证:B1C∥平面ADC1.
考点:直线与平面平行的判定,直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:(Ⅰ)证明BC⊥AC,CC1⊥BC,可得BC⊥平面AC1,即可证明BC⊥AC1;
(Ⅱ)连接A1C,A1C∩AC1=O,连接OD,证明OD∥B1C,即可证明B1C∥平面ADC1.
(Ⅱ)连接A1C,A1C∩AC1=O,连接OD,证明OD∥B1C,即可证明B1C∥平面ADC1.
解答:
证明:(Ⅰ)∵在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,BC?底面ABC,
∴CC1⊥BC,
∵AC=6,BC=8,AB=10,
∴BC⊥AC,
∵AC∩CC1=C,
∴BC⊥平面AC1,
∵AC1?平面AC1,
∴BC⊥AC1;
(Ⅱ)连接A1C,A1C∩AC1=O,连接OD,
∵点D是A1B1的中点,
∴OD∥B1C,
∵B1C?平面ADC1,OD?平面ADC1,
∴B1C∥平面ADC1.
∴CC1⊥BC,
∵AC=6,BC=8,AB=10,
∴BC⊥AC,
∵AC∩CC1=C,
∴BC⊥平面AC1,
∵AC1?平面AC1,
∴BC⊥AC1;
(Ⅱ)连接A1C,A1C∩AC1=O,连接OD,
∵点D是A1B1的中点,
∴OD∥B1C,
∵B1C?平面ADC1,OD?平面ADC1,
∴B1C∥平面ADC1.
点评:本题考查直线与平面平行,直线与平面垂直的判断与证明,考查空间想象能力,逻辑推理能力.

练习册系列答案
相关题目
若函数f(x)对任意a>0且a≠1,都有f(ax)=af(x),则称函数为“穿透”函数,则下列函数中,不是“穿透”函数的是( )
| A、f(x)=-x |
| B、f(x)=x+1 |
| C、f(x)=|x| |
| D、f(x)=x-|x| |
平面α的斜线l与它在这个平面上射影l′的方向向量分别为
=(1,0,1),
=(0,1,1),则斜线l与平面α所成的角为( )
| a |
| b |
| A、30° | B、45° |
| C、60° | D、90° |
各棱长均为a的三棱锥的表面积为( )
A、4
| ||
B、3
| ||
C、2
| ||
D、
|
函数E(x)定义如下:对任意x∈R,当x为有理数时,E(x)=1;当x为无理数时,E(x)=-1;则称函数E(x)为定义在实数上的狄利克雷拓展函数.下列关于函数E(x)说法错误的是( )
| A、E(x)的值域为{-1,1} | ||
| B、E(x)是偶函数 | ||
C、E(x)是周期函数且
| ||
| D、E(x)在实数集上的任何区间都不是单调函数 |
已知
+
=(2,
,2
),
-
=(0,
,0),则cos<
,
>=( )
| a |
| b |
| 2 |
| 3 |
| a |
| b |
| 2 |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
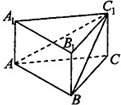 如图,在正三棱柱ABC-A1B1C1中,若AB=2,CC1=1,则点C到平面C1AB的距离等于
如图,在正三棱柱ABC-A1B1C1中,若AB=2,CC1=1,则点C到平面C1AB的距离等于