题目内容

计算sin
11π
4
的值为
 
．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：由条件利用诱导公式，对所给的式子进行化简，可得结果．
解答： 解：sin
11π
4
=sin（2π+
3π
4
）=sin
3π
4
=sin
π
4
=
2
2
，
故答案为：
2
2
．
点评：本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
相关题目
已知△ABC中，b=1，c=
2
，且
OA
+
AC
+
OB
=
0
（O是此三角形外心），则
AB
•
AO
=（　　）
A、-2B、-1C、1D、2
已知函数f（x）=x+
1
x
．
（Ⅰ）判断函数的奇偶性，并加以证明；
（Ⅱ）用定义证明f（x）在（0，1）上是减函数；
（Ⅲ）函数f（x）在[-1，0）上是否有最大值和最小值？如果有最大值或最小值，请求出最值．
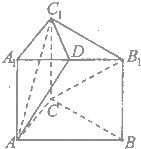如图在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=CC1=6，BC=8，AB=10，点D是A1B1的中点．
（Ⅰ）求证：BC⊥AC1；
（Ⅱ）求证：B1C∥平面ADC1．
函数f（x）=2sin
π
2
x与g（x）=
3x-2
图象所有交点的横坐标之和为（　　）
A、12B、14C、16D、18
在对人们休闲方式的一次调查中，共调查120人，其中女性70人、男性50人，女性中有40人主要的休闲方式是看电视，另外30人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外30人主要的休闲方式是运动．
（1）根据以上数据建立一个2×2的列联表；
（2）在犯错误的概率不超过0.10的前提下，认为休闲方式与性别是否有关？
参考数据：独立性检验临界值表
P（K2≥k0）0100.050.0250.0100.0050.001
k02.7063.8415.0246.6357.87910.828
独立性检验随机变量K2值的计算公式：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
（其中n=a+b+c+d）
设数列{an}的前n项和为Sn．已知a1=1，
2Sn
n
=an+1-
1
3
n2-n-
2
3
，n∈N*．
（1）求a2的值；
（2）求数列{an}的通项公式；
（3）证明：对一切正整数n，有
1
a1
+
1
a2
+…+
1
an
＜
7
4
．
已知角A，B，C是锐角△ABC的三个内角，若向量
m
=（cosA+sinA，2-2sinA），
n
=（cosA-sinA，1+sinA），且
m
⊥
n

（1）求角A；
（2）求函数y=2sin2B+cos（C-
1
2
A）的值域．
若a＞b＞0，c＞d＞0，则一定有（　　）
A、
a
c
＞
b
a
B、
a
c
＜
b
d
C、
a
d
＜
b
c
D、
a
d
＞
b
c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网