题目内容
函数E(x)定义如下:对任意x∈R,当x为有理数时,E(x)=1;当x为无理数时,E(x)=-1;则称函数E(x)为定义在实数上的狄利克雷拓展函数.下列关于函数E(x)说法错误的是( )
| A、E(x)的值域为{-1,1} | ||
| B、E(x)是偶函数 | ||
C、E(x)是周期函数且
| ||
| D、E(x)在实数集上的任何区间都不是单调函数 |
考点:分段函数的应用
专题:函数的性质及应用
分析:根据E(x)是周期函数,任意的有理数a都是E(x)的周期,任意的无理数都不是E(x)的周期,从而可得结论.
解答:
解:依题意,函数E(x)=
,
该函数的值域为{-1,1},E(-x)=E(x),则E(x)是偶函数,
显然E(x)是周期函数,任意的有理数a都是E(x)的周期,任意的无理数都不是E(x)的周期.
E(x)在实数集上的任何区间都不是单调函数.
故选C.
|
该函数的值域为{-1,1},E(-x)=E(x),则E(x)是偶函数,
显然E(x)是周期函数,任意的有理数a都是E(x)的周期,任意的无理数都不是E(x)的周期.
E(x)在实数集上的任何区间都不是单调函数.
故选C.
点评:本题主要考查了狄利克雷拓展函数,以及函数的周期性和单调性与奇偶性,同时考查了学生分析问题和解决问题的能力,以及运算求解的能力.

练习册系列答案
相关题目
已知x与y之间的一组数据:
则y与x的线性回归方程必过点的坐标为( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A、(1,2) |
| B、(2,3) |
| C、(1.5,4) |
| D、(1.5,3) |
已知偶数f(x)以4为周期,且当x∈[-2,0]时,f(x)=(
)x-1,若在区间[-6,6]内关于x的方程f(x)•log2(|x|+2)=0(a>1)恰有4个不同的实数根,则a的取值范围是( )
| 1 |
| 2 |
| A、(1,2) | |||
| B、(2,+∞) | |||
C、(1,
| |||
D、(
|
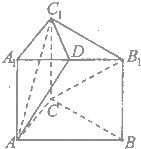 如图在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=CC1=6,BC=8,AB=10,点D是A1B1的中点.
如图在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=CC1=6,BC=8,AB=10,点D是A1B1的中点.