题目内容
平面α的斜线l与它在这个平面上射影l′的方向向量分别为
=(1,0,1),
=(0,1,1),则斜线l与平面α所成的角为( )
| a |
| b |
| A、30° | B、45° |
| C、60° | D、90° |
考点:直线与平面所成的角
专题:空间角
分析:根据线面角的定义,即平面的斜线与其在平面内的射影直线的夹角就是直线与平面所成的线面角,特别的线面平行或线在面内时为0弧度角,易知线面角的范围为[0,
],本题既然已经知道了直线与射影的直线的方向向量,则只需求出向量间的夹角即可,注意范围.
| π |
| 2 |
解答:
解:l与α所成的角为a与b所成的角(或其补角),
∵cos<
,
>=
=
,且<
,
>∈[0,
]
∴<a,b>=60°.
故答案为:60°.
∵cos<
| a |
| b |
| a•b |
| |a|•|b| |
| 1 |
| 2 |
| a |
| b |
| π |
| 2 |
∴<a,b>=60°.
故答案为:60°.
点评:本题考查了线面角的求法,要注意范围的限制条件.

练习册系列答案
相关题目
函数f(x)=2sin
x与g(x)=
图象所有交点的横坐标之和为( )
| π |
| 2 |
| 3 | x-2 |
| A、12 | B、14 | C、16 | D、18 |
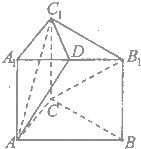 如图在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=CC1=6,BC=8,AB=10,点D是A1B1的中点.
如图在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=CC1=6,BC=8,AB=10,点D是A1B1的中点.