题目内容
11．
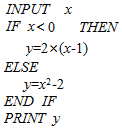执行表中的算法语句，若输入（INPUT）的x值为2，则输出（PRINT）的y值为2．
分析 算法的功能是计算y=$\left\{\begin{array}{l}{2（x-1）}&{x＜0}\\{{x}^{2}-2}&{x≥0}\end{array}\right.$的值，代入x=2，计算y的值即可得解．
解答 解：由程序语句知：算法的功能是计算y=$\left\{\begin{array}{l}{2（x-1）}&{x＜0}\\{{x}^{2}-2}&{x≥0}\end{array}\right.$的值，
当输入的x=2时，y=22-2=2．
故答案为：2．
点评 本题考查了选择结构的程序语句，根据语句判断算法的功能是解题的关键，属于基础题．
练习册系列答案
相关题目
2．某空调专卖店试销A、B、C三种新型空调，销售情况如表所示：
（1）求A型空调前三周的平均周销售量；
（2）根据C型空调前三周的销售情况，预估C型空调五周的平均周销售量为10台，当C型空调周销售量的方差最小时，求C4，C5的值；
（注：方差s2=$\frac{1}{n}$[x1-$\overline{x}$）2+（x${\;}_{2}-\overline{x}$）2+…+（xn-$\overline{x}$）2]，其中$\overline{x}$为x1，x2，…，xn的平均数）
（3）为跟踪调查空调的使用情况，根据销售记录，从第二周和第三周售出的空调中分别随机抽取一台，求抽取的两台空调中A型空调台数X的分布列及数学期望．
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量（台） | 11 | 10 | 15 | A4 | A5 |
| B型数量（台） | 10 | 12 | 13 | B4 | B5 |
| C型数量（台） | 15 | 8 | 12 | C4 | C5 |
（2）根据C型空调前三周的销售情况，预估C型空调五周的平均周销售量为10台，当C型空调周销售量的方差最小时，求C4，C5的值；
（注：方差s2=$\frac{1}{n}$[x1-$\overline{x}$）2+（x${\;}_{2}-\overline{x}$）2+…+（xn-$\overline{x}$）2]，其中$\overline{x}$为x1，x2，…，xn的平均数）
（3）为跟踪调查空调的使用情况，根据销售记录，从第二周和第三周售出的空调中分别随机抽取一台，求抽取的两台空调中A型空调台数X的分布列及数学期望．
3．已知命题：p“?x0∈R，x02+2ax0+a≤0”为假命题，则实数a的取值范围是（ ）
| A． | （0，1） | B． | [0，1] | C． | （1，2） | D． | （-∞，0）∪（1，+∞） |
20．已知（2x-1）10=a0+a1x+a2x2++a9x9+a10x10，求a2+a3+…+a9+a10的值为（ ）
| A． | -20 | B． | 0 | C． | 1 | D． | 20 |