题目内容
1.函数f(x)=(x-1)0+lg$\frac{1-x}{1+x}$的定义域是(-1,1).分析 根据函数f(x)的解析式,列出不等式组$\left\{\begin{array}{l}{x-1≠0}\\{\frac{1-x}{1+x}>0}\end{array}\right.$,解不等式组即可.
解答 解:∵函数f(x)=(x-1)0+lg$\frac{1-x}{1+x}$,
∴$\left\{\begin{array}{l}{x-1≠0}\\{\frac{1-x}{1+x}>0}\end{array}\right.$,
解得-1<x<1;
∴函数f(x)的定义域为(-1,1).
故答案为:(-1,1).
点评 本题考查了根据函数的解析式求定义域的应用问题,是基础题目.

练习册系列答案
相关题目
12.设i为虚数单位,已知复数z满足$\frac{z}{z-2i}$=i,则其共轭复数$\overline z$为( )
| A. | 1+i | B. | $\sqrt{2}$+$\sqrt{2}$i | C. | 1-i | D. | $\sqrt{2}$-$\sqrt{2}$i |
9.设集介A={x|1<($\frac{1}{2}$)x<8},B={x|y=lg(x2+3x+2)},从集合A中任取一个元素,则这个元素也是集合B中元素的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
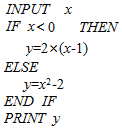 执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.
执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2. 已知函数f(x)=ax3+bx2+cx+d,其导函数的图象如图所示,则函数f(x)的图象只可能是( )
已知函数f(x)=ax3+bx2+cx+d,其导函数的图象如图所示,则函数f(x)的图象只可能是( )


