题目内容
19.正三棱锥P-ABC,侧棱长与底面边长相等,F是BC的中点,异面直线AC与PF所成的角为arccos$\frac{\sqrt{3}}{6}$.分析 作SO⊥底面ABC,交平面ABCD于点O,取AB中点E,取BC中点F,以O为原点,OE为x轴,OF为y轴,OS为z轴,建立空间直角坐标系,利用向量法能求出异面直线AC与PF所成的角.
解答 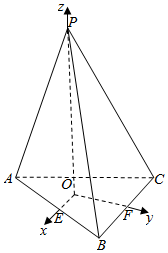 解:作SO⊥底面ABC,交平面ABCD于点O,取AB中点E,取BC中点F
解:作SO⊥底面ABC,交平面ABCD于点O,取AB中点E,取BC中点F
以O为原点,OE为x轴,OF为y轴,OS为z轴,建立空间直角坐标系,
设AB=BC=AC=SA=SB=SC=2,
则A(0,-$\frac{2\sqrt{3}}{3}$,0),C(-1,$\frac{\sqrt{3}}{3}$,0),
P(0,0,$\frac{2\sqrt{6}}{3}$),F(0,$\frac{\sqrt{3}}{3}$,0),
$\overrightarrow{AC}$=(-1,$\sqrt{3}$,0),$\overrightarrow{PF}$=(0,$\frac{\sqrt{3}}{3}$,-$\frac{2\sqrt{6}}{3}$),
设异面直线AC与PF所成的角为θ,
则cosθ=$\frac{|\overrightarrow{AC}•\overrightarrow{PF}|}{|\overrightarrow{AC}|•|\overrightarrow{PF}|}$=$\frac{1}{2\sqrt{3}}$=$\frac{\sqrt{3}}{6}$.
∴θ=arccos$\frac{\sqrt{3}}{6}$.
∴异面直线AC与PF所成的角为arccos$\frac{\sqrt{3}}{6}$.
点评 本题考查异面直线所成角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
9.已知集合A={x|-3<x<6},B={x|2<x<7},则A∩(∁RB)=( )
| A. | (2,6) | B. | (2,7) | C. | (-3,2] | D. | (-3,2) |
7.设函数f(x)=$\frac{2+|x|}{1+|x|}$,则使得f(2x)>f(x-3)成立的x的取值范围是( )
| A. | (-3,1) | B. | (-∞,-3)∪(1,+∞) | C. | (-3,+∞) | D. | (-∞,1) |
14.执行如图所示的程序框图,若输入的x值为2,则输出v的值为( )
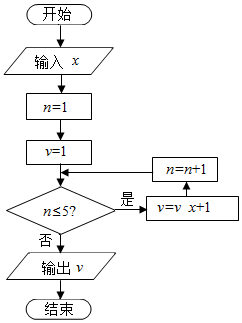

| A. | 31 | B. | 32 | C. | 63 | D. | 64 |
4.设α,β是两个不同的平面,l,m是两条不同的直线,α∩β=m,记α1为直线l与平面α所成的角,A={l|l?β},B={α1|l∈A},若对任意α1∈B,存在α${\;}_{{l}_{0}}$∈B,恒有α1<α${\;}_{{l}_{0}}$,则( )
| A. | α⊥β | B. | α与β不垂直 | C. | l0⊥a | D. | l0⊥m |
8.焦点为(6,0)且与双曲线$\frac{x^2}{2}$-y2=1有相同渐近线的双曲线的方程为( )
| A. | $\frac{{x}^{2}}{24}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{y}^{2}}{24}$-$\frac{{x}^{2}}{12}$=1 |
9.设集介A={x|1<($\frac{1}{2}$)x<8},B={x|y=lg(x2+3x+2)},从集合A中任取一个元素,则这个元素也是集合B中元素的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图则输出的值为( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图则输出的值为( )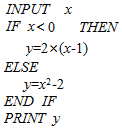 执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.
执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.