题目内容
16.已知$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(-1,3),则2$\overrightarrow{a}$+3$\overrightarrow{b}$的坐标为(1,7).分析 直接利用向量的坐标运算化简求解即可.
解答 解:$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(-1,3),
则2$\overrightarrow{a}$+3$\overrightarrow{b}$=2(2,-1)+3(-1,3)=(1,7).
故答案为:(1,7).
点评 本题考查向量的坐标运算,是基础题.

练习册系列答案
相关题目
6.设集合A={x|0<x<2},B={x|x2+x-2≥0},则A∩B=( )
| A. | (0,1] | B. | [1,2) | C. | [-2,2) | D. | (0,2) |
7.设函数f(x)=$\frac{2+|x|}{1+|x|}$,则使得f(2x)>f(x-3)成立的x的取值范围是( )
| A. | (-3,1) | B. | (-∞,-3)∪(1,+∞) | C. | (-3,+∞) | D. | (-∞,1) |
4.设α,β是两个不同的平面,l,m是两条不同的直线,α∩β=m,记α1为直线l与平面α所成的角,A={l|l?β},B={α1|l∈A},若对任意α1∈B,存在α${\;}_{{l}_{0}}$∈B,恒有α1<α${\;}_{{l}_{0}}$,则( )
| A. | α⊥β | B. | α与β不垂直 | C. | l0⊥a | D. | l0⊥m |
1.复数z=$\frac{(2i-3)(i-2)}{i}$的实部和虚部之和为( )
| A. | -3 | B. | 4 | C. | 3 | D. | -11 |
8.焦点为(6,0)且与双曲线$\frac{x^2}{2}$-y2=1有相同渐近线的双曲线的方程为( )
| A. | $\frac{{x}^{2}}{24}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{y}^{2}}{24}$-$\frac{{x}^{2}}{12}$=1 |
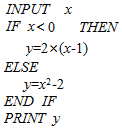 执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.
执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.