题目内容
2.某空调专卖店试销A、B、C三种新型空调,销售情况如表所示:| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量(台) | 11 | 10 | 15 | A4 | A5 |
| B型数量(台) | 10 | 12 | 13 | B4 | B5 |
| C型数量(台) | 15 | 8 | 12 | C4 | C5 |
(2)根据C型空调前三周的销售情况,预估C型空调五周的平均周销售量为10台,当C型空调周销售量的方差最小时,求C4,C5的值;
(注:方差s2=$\frac{1}{n}$[x1-$\overline{x}$)2+(x${\;}_{2}-\overline{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$为x1,x2,…,xn的平均数)
(3)为跟踪调查空调的使用情况,根据销售记录,从第二周和第三周售出的空调中分别随机抽取一台,求抽取的两台空调中A型空调台数X的分布列及数学期望.
分析 (1)根据平均数公式计算即可,
(2)根据方差的定义可得S2=$\frac{1}{5}$[2(c4-$\frac{15}{2}$)+$\frac{91}{2}$],根据二次函数性质求出c4=7或c4=8时,S2取得最小值,
(3)依题意,随机变量 的可能取值为 0,1,2,求出P,列出分布表,求出数学期望.
解答 解:(1)A型空调前三周的平均周销售量$\overline{x}$=$\frac{1}{5}$(11+10+15)=12台,
(2)因为C型空调平均周销量为10台,
所以c4+c5=10×15-15-8-12=15,
又S2=$\frac{1}{5}$[(15-10)2+(8-10)2+(12-10)2+(c4-10)2+(c5-10)2],
化简得到S2=$\frac{1}{5}$[2(c4-$\frac{15}{2}$)+$\frac{91}{2}$],
因为c4∈N,
所以c4=7或c4=8时,S2取得最小值,
此时C5=8或C5=7,
(3)依题意,随机变量 的可能取值为 0,1,2,
P(X=0)=$\frac{20}{30}$×$\frac{25}{40}$=$\frac{5}{12}$,
P(X=1)=$\frac{10}{30}$×$\frac{25}{40}$+$\frac{20}{30}$×$\frac{15}{40}$=$\frac{11}{24}$,
P(X=2)=$\frac{10}{30}$×$\frac{15}{40}$=$\frac{1}{8}$,
随机变量的X的分布列,
| X | 0 | 1 | 2 |
| P | $\frac{5}{12}$ | $\frac{11}{24}$ | $\frac{1}{8}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
7.设函数f(x)=$\frac{2+|x|}{1+|x|}$,则使得f(2x)>f(x-3)成立的x的取值范围是( )
| A. | (-3,1) | B. | (-∞,-3)∪(1,+∞) | C. | (-3,+∞) | D. | (-∞,1) |
14.执行如图所示的程序框图,若输入的x值为2,则输出v的值为( )
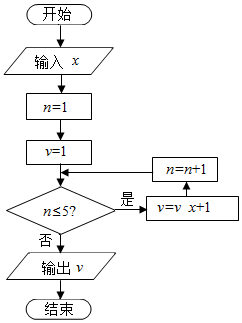

| A. | 31 | B. | 32 | C. | 63 | D. | 64 |
12.设i为虚数单位,已知复数z满足$\frac{z}{z-2i}$=i,则其共轭复数$\overline z$为( )
| A. | 1+i | B. | $\sqrt{2}$+$\sqrt{2}$i | C. | 1-i | D. | $\sqrt{2}$-$\sqrt{2}$i |
 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图则输出的值为( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图则输出的值为( )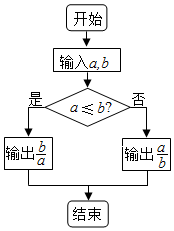
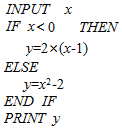 执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.
执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.