题目内容
6.计算:tan15°tan30°tan45°tan75°.分析 根据题意,先由特殊角的三角函数值可得tan30°=$\frac{\sqrt{3}}{3}$,tan45°=1,而tan15°tan75°=$\frac{sin15°}{cos15°}$×$\frac{sin75°}{cos75°}$=$\frac{sin15°}{cos15°}$×$\frac{cos15°}{sin15°}$=1,代入tan15°tan30°tan45°tan75°中计算即可得答案.
解答 解:根据题意,原式=tan15°tan30°tan45°tan75°=$\frac{\sqrt{3}}{3}$×tan15°tan75°=$\frac{\sqrt{3}}{3}$×$\frac{sin15°}{cos15°}$×$\frac{sin75°}{cos75°}$=$\frac{\sqrt{3}}{3}$×$\frac{sin15°}{cos15°}$×$\frac{cos15°}{sin15°}$=$\frac{\sqrt{3}}{3}$;
故tan15°tan30°tan45°tan75°=$\frac{\sqrt{3}}{3}$.
点评 本题考查同角三角函数基本关系式的运用,涉及特殊角的三角函数值,解题的关键是利用诱导公式计算tan15°tan75°的值.

练习册系列答案
相关题目
16.若关于x的不等式xex-ax+a<0的解集为(m,n)(n<0),且(m,n)中只有一个整数,则实数a的取值范围是( )
| A. | [$\frac{1}{{e}^{2}}$,$\frac{1}{e}$) | B. | [$\frac{2}{3{e}^{2}}$,$\frac{1}{2e}$) | C. | [$\frac{1}{{e}^{2}}$,$\frac{2}{e}$) | D. | [$\frac{2}{3{e}^{2}}$,$\frac{1}{e}$) |
14.执行如图所示的程序框图,若输入的x值为2,则输出v的值为( )
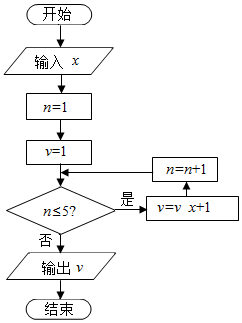

| A. | 31 | B. | 32 | C. | 63 | D. | 64 |
1.直线m:x+(a2-1)y+1=0,直线n:x+(2-2a)y-1=0,则“a=-3”是“直线m、n关于原点对称”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
18.将函数f(x)=sin2x的图象向左平移$\frac{π}{6}$个单位后与函数g(x)的图象重合,则函数g(x)为( )
| A. | $sin(2x-\frac{π}{6})$ | B. | $sin(2x+\frac{π}{6})$ | C. | $sin(2x-\frac{π}{3})$ | D. | $sin(2x+\frac{π}{3})$ |
15.在各项均为正数的等比数列{an}中,a5a6=4,则数列{log2an}的前10项和等于( )
| A. | 20 | B. | 10 | C. | 5 | D. | 2+log25 |
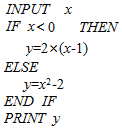 执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.
执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.