题目内容
1.设函数f(x)=$\frac{1}{{2}^{x}+\sqrt{2}}$,类比课本中推导等差数列前n项和公式的方法,可求得f(-2015)+f(-2014)+f(-2013)+…+f(2014)+f(2015)+f(2016)的值为1008$\sqrt{2}$.分析 根据课本中推导等差数列前n项和的公式的方法-倒序相加法,观察所求式子的特点,应先求f(x)+f(1-x)的值,从而求出即可.
解答 解:∵f(x)=$\frac{1}{{2}^{x}+\sqrt{2}}$,
∴f(x)+f(1-x)
=$\frac{1}{{2}^{x}+\sqrt{2}}$+$\frac{1}{{2}^{1-x}+\sqrt{2}}$
=$\frac{1}{{2}^{x}+\sqrt{2}}$+$\frac{{2}^{x}}{2+\sqrt{2}{•2}^{x}}$
=$\frac{{2}^{x}+\sqrt{2}}{\sqrt{2}{(2}^{x}+\sqrt{2})}$=$\frac{\sqrt{2}}{2}$,
即 f(-2015)+f(2016)=$\frac{\sqrt{2}}{2}$,
f(-2014)+f(2015)=$\frac{\sqrt{2}}{2}$,
f(-2013)+f(2014)=$\frac{\sqrt{2}}{2}$,
…,
f(-2)+f(3)=$\frac{\sqrt{2}}{2}$,
f(-1)+f(2)=$\frac{\sqrt{2}}{2}$,
f(0)+f(1)=$\frac{\sqrt{2}}{2}$,
∴f(-2015)+f(-2014)+f(-2013)+…+f(2014)+f(2015)+f(2016)=2016×$\frac{\sqrt{2}}{2}$=1008$\sqrt{2}$,
故答案为:1008$\sqrt{2}$.
点评 本题为规律性的题目,要善于观察式子的特点,并且此题给出了明确的方法,从而降低了本题难度.

练习册系列答案
相关题目
9.已知集合A={x|-3<x<6},B={x|2<x<7},则A∩(∁RB)=( )
| A. | (2,6) | B. | (2,7) | C. | (-3,2] | D. | (-3,2) |
16.若关于x的不等式xex-ax+a<0的解集为(m,n)(n<0),且(m,n)中只有一个整数,则实数a的取值范围是( )
| A. | [$\frac{1}{{e}^{2}}$,$\frac{1}{e}$) | B. | [$\frac{2}{3{e}^{2}}$,$\frac{1}{2e}$) | C. | [$\frac{1}{{e}^{2}}$,$\frac{2}{e}$) | D. | [$\frac{2}{3{e}^{2}}$,$\frac{1}{e}$) |
6.设集合A={x|0<x<2},B={x|x2+x-2≥0},则A∩B=( )
| A. | (0,1] | B. | [1,2) | C. | [-2,2) | D. | (0,2) |
 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图则输出的值为( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图则输出的值为( )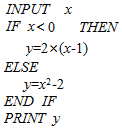 执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.
执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.