题目内容
20.已知(2x-1)10=a0+a1x+a2x2++a9x9+a10x10,求a2+a3+…+a9+a10的值为( )| A. | -20 | B. | 0 | C. | 1 | D. | 20 |
分析 本题由于是求二项式展开式的系数之和,故可以令二项式中的x=1,又由于所求之和不含a0,令x=0,可求出a0的值,再求出a1=-20,代入即求答案.
解答 解:令x=1得,a0+a1+a2+…+a9+a10=1,
再令x=0得,a0=1,所以a1+a2+…+a9+a10=0,
又因为a1=${C}_{20}^{19}•2•(-1)^{19}$=-20,代入得a2+a3+…+a9+a10=20.
故选:D.
点评 本题主要考查二项式定理的应用,一般在求解有二项式关系数的和等问题时通常会将二项式展开式中的未知数x赋值为1或0或者是-1进行求解.本题属于基础题型.

练习册系列答案
相关题目
8.焦点为(6,0)且与双曲线$\frac{x^2}{2}$-y2=1有相同渐近线的双曲线的方程为( )
| A. | $\frac{{x}^{2}}{24}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{y}^{2}}{24}$-$\frac{{x}^{2}}{12}$=1 |
15.在各项均为正数的等比数列{an}中,a5a6=4,则数列{log2an}的前10项和等于( )
| A. | 20 | B. | 10 | C. | 5 | D. | 2+log25 |
12.设i为虚数单位,已知复数z满足$\frac{z}{z-2i}$=i,则其共轭复数$\overline z$为( )
| A. | 1+i | B. | $\sqrt{2}$+$\sqrt{2}$i | C. | 1-i | D. | $\sqrt{2}$-$\sqrt{2}$i |
9.设集介A={x|1<($\frac{1}{2}$)x<8},B={x|y=lg(x2+3x+2)},从集合A中任取一个元素,则这个元素也是集合B中元素的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图则输出的值为( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图则输出的值为( )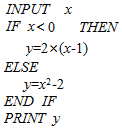 执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.
执行表中的算法语句,若输入(INPUT)的x值为2,则输出(PRINT)的y值为2.