题目内容
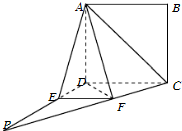如图，四边形ABCD为正方形．PD⊥平面ABCD，∠DPC=30°，AF⊥PC于点F，FE∥CD，交PD于点E．（1）证明：CF⊥平面ADF；
（2）求二面角D-AF-E的余弦值．
考点：用空间向量求平面间的夹角,直线与平面垂直的判定,二面角的平面角及求法
专题：空间位置关系与距离,空间向量及应用
分析：（1）结合已知又直线和平面垂直的判定定理可判PC⊥平面ADF，即得所求；
（2）由已知数据求出必要的线段的长度，建立空间直角坐标系，由向量法计算即可．
（2）由已知数据求出必要的线段的长度，建立空间直角坐标系，由向量法计算即可．
解答：
解：（1）∵PD⊥平面ABCD，∴PD⊥AD，
又CD⊥AD，PD∩CD=D，∴AD⊥平面PCD，
∴AD⊥PC，又AF⊥PC，
∴PC⊥平面ADF，即CF⊥平面ADF；
（2）设AB=1，在RT△PDC中，CD=1，∠DPC=30°，
∴PC=2，PD=
，由（1）知CF⊥DF，
∴DF=
，AF=
=
，
∴CF=
=
，又FE∥CD，
∴
=
=
，∴DE=
，同理可得EF=
CD=
，
如图所示，以D为原点，建立空间直角坐标系，
则A（0，0，1），E（
，0，0），F（
，
，0），P（
，0，0），C（0，1，0）
设向量
=（x，y，z）为平面AEF的法向量，则有
⊥
，
⊥
，
∴
，令x=4可得z=
，∴
=（4，0，
），
由（1）知平面ADF的一个法向量为
=（-
，1，0），
设二面角D-AF-E的平面角为θ，可知θ为锐角，
cosθ=|cos＜
，
＞|=
=
=
∴二面角D-AF-E的余弦值为：
又CD⊥AD，PD∩CD=D，∴AD⊥平面PCD，
∴AD⊥PC，又AF⊥PC，
∴PC⊥平面ADF，即CF⊥平面ADF；
（2）设AB=1，在RT△PDC中，CD=1，∠DPC=30°，
∴PC=2，PD=
| 3 |
∴DF=
| ||
| 2 |
| AD2+DF2 |
| ||
| 2 |
∴CF=
| AC2-AF2 |
| 1 |
| 2 |
∴
| DE |
| PD |
| CF |
| PC |
| 1 |
| 4 |
| ||
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
如图所示，以D为原点，建立空间直角坐标系，
则A（0，0，1），E（
| ||
| 4 |
| ||
| 4 |
| 3 |
| 4 |
| 3 |
设向量
| m |
| m |
| AE |
| m |
| EF |
∴
|
| 3 |
| m |
| 3 |
由（1）知平面ADF的一个法向量为
| PC |
| 3 |
设二面角D-AF-E的平面角为θ，可知θ为锐角，
cosθ=|cos＜
| m |
| PC |
|
| ||||
|
|
4
| ||
|
2
| ||
| 19 |
∴二面角D-AF-E的余弦值为：
2
| ||
| 19 |
点评：本题考查用空间向量法求二面角的余弦值，建立空间直角坐标系并准确求出相关点的坐标是解决问题的关键，属中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知函数f（x）=3ex-x2ex-a在R上存在三个零点，则实数a的取值范围为（ ）
| A、[6e-3，2e] |
| B、（0，2e] |
| C、（-6e-3，0） |
| D、（-6e-3，2e） |
已知数列{an}的前n项和Sn=n2-2n，令bn=ancos
，记数列{bn}的前n项和为Tn，则T2014=（ ）
| nπ |
| 2 |
| A、-2011 |
| B、-2012 |
| C、-2013 |
| D、-2014 |
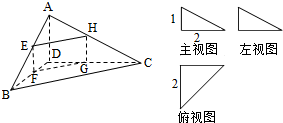四面体ABCD及其三视图如图所示，平行于棱AD，BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H．
如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD是等腰梯形，∠DAB=60°，AB=2CD=2，M是线段AB的中点．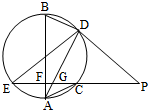
如图，EP交圆于E，C两点，PD切圆于D，G为CE上一点且PG=PD，连接DG并延长交圆于点A，作弦AB垂直EP，垂足为F．