题目内容
已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)-f(y)|<
|x-y|.
若对所有x,y∈[0,1],|f(x)-f(y)|<m恒成立,则m的最小值为( )
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有|f(x)-f(y)|<
| 1 |
| 2 |
若对所有x,y∈[0,1],|f(x)-f(y)|<m恒成立,则m的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数恒成立问题,绝对值不等式的解法
专题:综合题,函数的性质及应用
分析:依题意,构造函数f(x)=
(0<k<
),分x∈[0,
],且y∈[0,
];x∈[0,
],且y∈[
,1];y∈[0,
],且y∈[
,1];及当x∈[
,1],且y∈[
,1]时,四类情况讨论,可证得对所有x,y∈[0,1],|f(x)-f(y)|<
恒成立,从而可得m≥
,继而可得答案.
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:依题意,定义在[0,1]上的函数y=f(x)的斜率|k|<
,
依题意,k>0,构造函数f(x)=
(0<k<
),满足f(0)=f(1)=0,|f(x)-f(y)|<
|x-y|.
当x∈[0,
],且y∈[0,
]时,|f(x)-f(y)|=|kx-ky|=k|x-y|≤k|
-0|=k×
<
;
当x∈[0,
],且y∈[
,1],|f(x)-f(y)|=|kx-(k-ky)|=|k(x+y)-k|≤|k(1+
)-k|=
<
;
当y∈[0,
],且x∈[
,1]时,同理可得,|f(x)-f(y)|<
;
当x∈[
,1],且y∈[
,1]时,|f(x)-f(y)|=|(k-kx)-(k-ky)|=k|x-y|≤k×(1-
)=
<
;
综上所述,对所有x,y∈[0,1],|f(x)-f(y)|<
,
∵对所有x,y∈[0,1],|f(x)-f(y)|<m恒成立,
∴m≥
,即m的最小值为
.
故选:B.
| 1 |
| 2 |
依题意,k>0,构造函数f(x)=
|
| 1 |
| 2 |
| 1 |
| 2 |
当x∈[0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
当x∈[0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 4 |
当y∈[0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
当x∈[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 4 |
综上所述,对所有x,y∈[0,1],|f(x)-f(y)|<
| 1 |
| 4 |
∵对所有x,y∈[0,1],|f(x)-f(y)|<m恒成立,
∴m≥
| 1 |
| 4 |
| 1 |
| 4 |
故选:B.
点评:本题考查函数恒成立问题,着重考查构造函数思想、分类讨论思想、函数方程思想与等价转化思想的综合运用,考查分析、推理及运算能力,属于难题.

练习册系列答案
相关题目
已知数列{an},an=-2n2+λn,若该数列是递减数列,则实数λ的取值范围是( )
| A、(-∞,6) |
| B、(-∞,4] |
| C、(-∞,5) |
| D、(-∞,3] |
已知函数f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4 |
| 2015 |
| 2014 |
| 2015 |
| A、1007 | B、2014 |
| C、2015 | D、4028 |
已知数列{an}的前n项和Sn=n2-2n,令bn=ancos
,记数列{bn}的前n项和为Tn,则T2014=( )
| nπ |
| 2 |
| A、-2011 |
| B、-2012 |
| C、-2013 |
| D、-2014 |
已知sinα=
,则cos2α-cos2α的值为( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
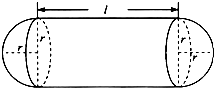 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为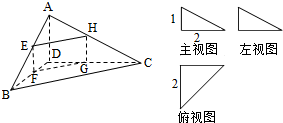 四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H.
四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H. 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.