题目内容
设0<ω<4,函数f(x)=sin(ωx+φ)的图象若向右平移
个单位所得到的图象与原图象重合,若向左平移
个单位所得到的图象关于y轴对称,则tan(ωφ)的值为 .
| 2π |
| 3 |
| π |
| 12 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据函数f(x)=sin(x+φ)的图象若向右平移
个单位所得到的图象与原图象重合,可得
=k•
,k∈N,结合ω的范围,可得ω 的值.根据f(x)的图象向左平移
个单位所得到的图象关于y轴对称,可得y=sin[3(x+
)+φ]为偶函数,可得 φ+
=kπ+
,k∈z,由此求得φ 的值,从而求得tan(ωφ)的值.
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| ω |
| π |
| 12 |
| π |
| 12 |
| π |
| 4 |
| π |
| 2 |
解答:
解:∵函数f(x)=sin(x+φ)的图象若向右平移
个单位所得到的图象与原图象重合,
∴
=k•
,k∈N,∴ω=3k.
结合0<ω<4,可得ω=3.
∵f(x)的图象向左平移
个单位所得到的图象关于y轴对称,故所得函数为偶函数,
∴y=sin[3(x+
)+φ]=sin(3x+φ+
)为偶函数,∴φ+
=kπ+
,k∈z.
故可取φ=
.
tan(ωφ)=tan
=-1,
故答案为:-1.
| 2π |
| 3 |
∴
| 2π |
| 3 |
| 2π |
| ω |
结合0<ω<4,可得ω=3.
∵f(x)的图象向左平移
| π |
| 12 |
∴y=sin[3(x+
| π |
| 12 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
故可取φ=
| π |
| 4 |
tan(ωφ)=tan
| 3π |
| 4 |
故答案为:-1.
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,函数y=Asin(ωx+φ)的图象的周期性和对称性,属于中档题.

练习册系列答案
相关题目
某三棱锥的三视图如图所示,则该几何体的体积为( )
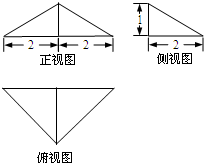

A、
| ||
B、
| ||
C、
| ||
| D、4 |
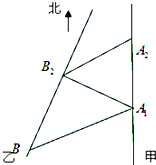 如图,甲船以每小时15
如图,甲船以每小时15