题目内容
图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔AB、CD与桥面AC垂直,通过测量得知AB=50m,AC=50m,当P为AC中点时,∠BPD=45°.
(1)求CD的长;
(2)试问P在线段AC的何处时,∠BPD达到最大.
(1)求CD的长;
(2)试问P在线段AC的何处时,∠BPD达到最大.

考点:解三角形的实际应用
专题:应用题,解三角形
分析:(1)设∠BPA=α,∠DPC=β,CD=h,则tanα=2,tanβ=
,利用∠BPD=45°,可求CD的长;
(2)设AP=x(0<x<50),则tanα=
,tanβ=
,可得tan∠BPD,换元,利用基本不等式,即可求出∠BPD最大,从而可得结论.
| h |
| 25 |
(2)设AP=x(0<x<50),则tanα=
| 50 |
| x |
| 75 |
| 50-x |
解答:
解:(1)设∠BPA=α,∠DPC=β,CD=h,则tanα=2,tanβ=
,
由题意得,tan(α+β)=
=-1,解得CD=h=75.…(6分)
(2)设AP=x(0<x<50),则tanα=
,tanβ=
,
∴tan∠BPD=-tan(α+β)=-
=
,…(8分)
∵x2-50x+50•75>0,∴tan∠BPD>0,即∠BPD为锐角,
令t=x+100∈(100,150),则x=t-100,
∴tan∠BPD=
=
,
∴tan∠BPD=
≤
=
,…(12分)
当且仅当t=
即t=25
∈(100,150),
∴AP=25
-100时,∠BPD最大.…(14分)
| h |
| 25 |
由题意得,tan(α+β)=
2+
| ||
1-2•
|
(2)设AP=x(0<x<50),则tanα=
| 50 |
| x |
| 75 |
| 50-x |
∴tan∠BPD=-tan(α+β)=-
| ||||
1-
|
| 25(x+100) |
| x2-50x+50•75 |
∵x2-50x+50•75>0,∴tan∠BPD>0,即∠BPD为锐角,
令t=x+100∈(100,150),则x=t-100,
∴tan∠BPD=
| 25t |
| (t-100)2-50(t-100)+50•75 |
| 25t |
| t2-250t+50•375 |
∴tan∠BPD=
| 25 | ||
t+
|
| 25 | ||||
2
|
| 1 | ||
2
|
当且仅当t=
| 50•375 |
| t |
| 30 |
∴AP=25
| 30 |
点评:本题考查解三角形的实际应用,考查和角的正切公式,考查基本不等式的运用,求出tan∠BPD是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设i为虚数单位,复数z的共轭复数为
,且(
-1)(1+i)=2i,则复数z的模为( )
. |
| z |
. |
| z |
| A、5 | ||
B、
| ||
| C、2-i | ||
| D、1 |
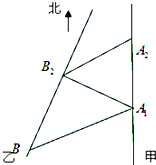 如图,甲船以每小时15
如图,甲船以每小时15