题目内容
已知22x-4•2x>m-5,求m的取值范围.
考点:指、对数不等式的解法
专题:不等式的解法及应用
分析:令t=2x>0,可得 m<t2-4t+5,利用二次函数的性质求得t2-4t+5 的最小值为1,可得m的取值范围.
解答:
解:令t=2x>0,可得 m<t2-4t+5,由于t2-4t+5=(t-2)2+1≥1,
故m<1.
故m<1.
点评:本题主要考查指数函数的定义域和值域,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
集合A={x|0<2x-1<3},B={x|-1<1og
x<0},则A∩(∁RB)=( )
| 1 |
| 2 |
| A、(0,1] |
| B、(1,2) |
| C、(-∞,0)∪(2,+∞) |
| D、∅ |
已知集合{a,
,1}={a2,a+b,0},则a251+b252的值是( )
| b |
| a |
| A、-1 | B、0 | C、1 | D、2 |
定义域为R的奇函数f(x),当x∈(-∞,0)时f(x)+xf′(x)<0恒成立,若a=2f(2),b=ln2•f(ln2),c=-f(-1),则a,b,c的大小关系为( )
| A、a>b>c |
| B、c>b>a |
| C、a>c>b |
| D、b>c>a |
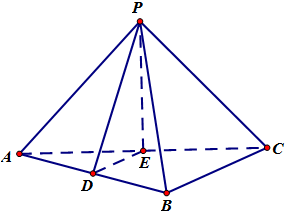 如图,在三棱锥P-ABC中,AB⊥BC,D,E分别是AB,AC的中点,且PE⊥平面ABC.求证:
如图,在三棱锥P-ABC中,AB⊥BC,D,E分别是AB,AC的中点,且PE⊥平面ABC.求证: