题目内容
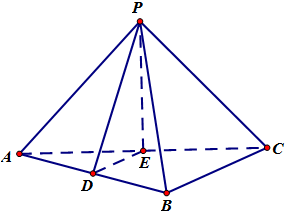如图，在三棱锥P-ABC中，AB⊥BC，D，E分别是AB，AC的中点，且PE⊥平面ABC．求证：（1）BC∥平面PDE；
（2）AB⊥平面PDE．
考点：直线与平面平行的判定,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）根据线面平行的判定定理即可证明BC∥平面PDE；
（2）根据线面垂直的判定定理即可证明AB⊥平面PDE．
（2）根据线面垂直的判定定理即可证明AB⊥平面PDE．
解答：
证明：（1）∵D，E分别是AB，AC的中点，
∴DE∥BC，
∵BC?平面PDE，DE?平面PDE，
∴BC∥平面PDE；
（2）∵PE⊥平面ABC，AB?平面ABC，
∴PE⊥AB，
∵DE∥BC，AB⊥BC，
∴DE⊥AB，
∵PE∩DE=E，
∴AB⊥平面PDE．
∴DE∥BC，
∵BC?平面PDE，DE?平面PDE，
∴BC∥平面PDE；
（2）∵PE⊥平面ABC，AB?平面ABC，
∴PE⊥AB，
∵DE∥BC，AB⊥BC，
∴DE⊥AB，
∵PE∩DE=E，
∴AB⊥平面PDE．
点评：本题主要考查空间直线和平面的位置关系的判断，根据线面垂直和线面平行的判定定理是解决本题的关键．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
若x≥0，y≥0，且x+2y=1，则2x+3y的最小值为（ ）
| A、2 | ||
B、
| ||
C、
| ||
| D、0 |
如图，直三棱柱ABC-A1B1C1中，底面△ABC边长分别为AC=3，BC=4，AB=5，D为AB中点，AA1=4，BC1与B1C交于点O．已知M=
（a，θ∈R，a≠0），则M的最大值与最小值分别为（ ）
| a2+asinθ+1 |
| a2+acosθ+1 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|