题目内容
已知函数f（x）=loga（x+3）在区间[-2，-1]上总有|f（x）|＜2，求实数a的取值范围．
考点：对数函数的值域与最值
专题：函数的性质及应用
分析：根据对数的性质以及绝对值的解法解不等式即可得到结论．
解答：
解：当-2≤x≤-1，1≤x+3≤2，∫
由|f（x）|＜2，
∴-2＜f（x）＜2，
即-2＜loga（x+3）＜2恒成立，
若a＞1时，0=loga1≤loga（x+3）≤loga2，
此时有loga2＜2，
解得a＞
，
若0＜a＜1时，0=loga1≥loga（x+3）≥loga2，
此时有loga2＞-2，
解得0＜a＜
，
综上：a＞
，或0＜a＜
．
| 3 |
| 4 |
由|f（x）|＜2，
∴-2＜f（x）＜2，
即-2＜loga（x+3）＜2恒成立，
若a＞1时，0=loga1≤loga（x+3）≤loga2，
此时有loga2＜2，
解得a＞
| 2 |
若0＜a＜1时，0=loga1≥loga（x+3）≥loga2，
此时有loga2＞-2，
解得0＜a＜
| ||
| 2 |
综上：a＞
| 2 |
| ||
| 2 |
点评：本题主要考查不等式恒成立问题，根据条件结合对数的运算性质是解决本题的关键，考查学生的计算能力．
练习册系列答案
相关题目
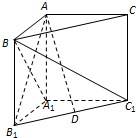如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1．