Question

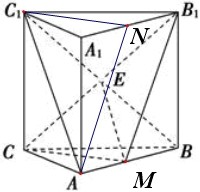
三棱柱ABC-A₁B₁C₁中，M为AB的中点，N为A₁B₁的中点．
（1）求证：AC₁∥平面B₁MC；
（2）求证：平面ANC₁∥平面B₁MC．

Answer 1

考点：平面与平面平行的判定,直线与平面平行的判定

专题：空间位置关系与距离

分析：（1）连接BC₁，交B₁C于点E，连接ME，则BC₁与B₁C互相平分，从而BE=C₁E，又AM=BM，根据中位线定理可知AC₁∥ME，又ME?平面CMB₁，AC₁?平面B₁MC，最后根据线面平行的判定定理可知AC₁∥平面B₁MC．
（2）利用直线与平面平行的判定定理可得AN∥平面B₁MC．又由（1）知，AC₁∥平面CMB₁．根据平面与平面平行的判定定理可得平面ANC₁∥平面B₁MC．

解答： 证明：（1）证明：连接BC₁，交B₁C于点E，连接DE，则BC₁与B₁C互相平分．
∴BE=C₁E，又AM=BM，
∴ME为△ABC₁的中位线，
∴AC₁∥ME．
又ME?平面CMB₁，AC₁?平面CMB₁，
∴AC₁∥平面CMB₁．
（2）三棱柱ABC-A₁B₁C₁中，
∵M为AB的中点，N为A₁B₁的中点，
∴AM∥B₁N，且AM=B₁N，
∴四边形AMB₁N是平行四边形．
∴AN∥B₁M．
又∵B₁M?平面B₁MC，
AN?平面B₁MC．
∴AN∥平面B₁MC．
由（1）知，AC₁∥平面CMB₁，
∴平面ANC₁∥平面B₁MC．

点评：本题考查直线与平面平行的判定定理以及平面与平面平行的判定定理的应用．属于中档题．