题目内容
已知函数f(x)=2x+
|x|.
(1)解不等式:
≤f(x)≤
;
(2)若关于x的方程f(2x)+af(x)+4=0在(0,+∞)上有解,求实数a的取值范围.
| 1 |
| 2 |
(1)解不等式:
| ||
| 2 |
| 17 |
| 4 |
(2)若关于x的方程f(2x)+af(x)+4=0在(0,+∞)上有解,求实数a的取值范围.
考点:指数函数综合题
专题:函数的性质及应用,不等式的解法及应用
分析:(1)将函数表示为分段函数形式,然后根据分段函数即可解不等式:
≤f(x)≤
;
(2)利用换元法将方程转化为关于t的方程形式,然后利用基本不等式即可得到结论.
| ||
| 2 |
| 17 |
| 4 |
(2)利用换元法将方程转化为关于t的方程形式,然后利用基本不等式即可得到结论.
解答:
解:(1)当x≤0时,f(x)=2x+
|x|=2•2x=2x+1≤2,
当x>0时,f(x)=2x+(
)x≥2
=2.
∴由不等式
≤f(x)≤
得:
当x≤0等价为
≤2x+1,即2 -
≤2x+1,
∴x+1≥-
,即-
≤x≤0,
当x>0等价为2x+(
)x≤
,
设t=2x,则t>1,
∴t+
≤
,
即4t2-17t+4≤0,
解得
≤t≤4,此时1<t≤4,
此时1<2x≤4,解得0<x≤2.
综上不等式的解为-
≤x≤2,即不等式的解集为{x|-
≤x≤2}.
(2)∵当x>0时,f(x)=2x+(
)x.
∴f(2x)+af(x)+4=0在(0,+∞)上等价为:
[22x+(
)2x]+a[2x+(
)x]+4=0,
即[2x+(
)x]2+a[2x+(
)x]+2=0,①
设t=2x+(
)x,则当x>0时,t>2,
此时方程①等价为t2+at+2=0,
即a=
=-(t+
),
∵当t>2时,g(t)=t+
单调递增,
∴g(t)>g(2)=3,
∴-g(t)=-(t+
)<-3,
∴要使a=
=-(t+
)有解,则a<-3,
即实数a的取值范围是a<-3.
| 1 |
| 2 |
当x>0时,f(x)=2x+(
| 1 |
| 2 |
2x•(
|
∴由不等式
| ||
| 2 |
| 17 |
| 4 |
当x≤0等价为
| ||
| 2 |
| 1 |
| 2 |
∴x+1≥-
| 1 |
| 2 |
| 3 |
| 2 |
当x>0等价为2x+(
| 1 |
| 2 |
| 17 |
| 4 |
设t=2x,则t>1,
∴t+
| 1 |
| t |
| 17 |
| 4 |
即4t2-17t+4≤0,
解得
| 1 |
| 4 |
此时1<2x≤4,解得0<x≤2.
综上不等式的解为-
| 3 |
| 2 |
| 3 |
| 2 |
(2)∵当x>0时,f(x)=2x+(
| 1 |
| 2 |
∴f(2x)+af(x)+4=0在(0,+∞)上等价为:
[22x+(
| 1 |
| 2 |
| 1 |
| 2 |
即[2x+(
| 1 |
| 2 |
| 1 |
| 2 |
设t=2x+(
| 1 |
| 2 |
此时方程①等价为t2+at+2=0,
即a=
| -t2-2 |
| t |
| 2 |
| t |
∵当t>2时,g(t)=t+
| 2 |
| t |
∴g(t)>g(2)=3,
∴-g(t)=-(t+
| 2 |
| t |
∴要使a=
| -t2-2 |
| t |
| 2 |
| t |
即实数a的取值范围是a<-3.
点评:本题主要考查不等式的解法以及基本不等式的应用,将函数表示为分段函数形式,利用换元法是解决本题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
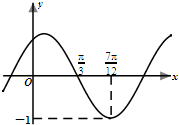 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<