题目内容
设函数f(x)=|x+1|+|x-a|(a>0).
(1)若不等式f(x)≥5的解集为{x|x≤-2或x≥3},求a的值;
(2)若不等式f(x)≥6恒成立,求a的范围.
(1)若不等式f(x)≥5的解集为{x|x≤-2或x≥3},求a的值;
(2)若不等式f(x)≥6恒成立,求a的范围.
考点:绝对值不等式的解法,函数恒成立问题
专题:计算题,不等式的解法及应用
分析:(1)运用分段函数表示函数f(x),由题设知:|x+1|+|x-a|≥5,在同一坐标系中作出函数y=5的图象,当x=-2或3时,f(x)=5,且a+1<5即a<4,由f(-2)=5 求得a的值;
(2)由绝对值不等式的性质,可得f(x)的最小值为|a+1|,令6不大于最小值,解不等式即可得到a的范围.
(2)由绝对值不等式的性质,可得f(x)的最小值为|a+1|,令6不大于最小值,解不等式即可得到a的范围.
解答:
 解:(1)f(x)=|x+1|+|x-a|=
解:(1)f(x)=|x+1|+|x-a|=
,
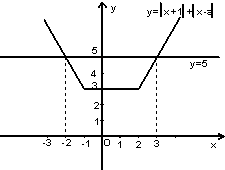
函数f(x)如图所示.
由题设知:|x+1|+|x-a|≥5解集为(-∞,-2]∪[3,+∞).
如图,在同一坐标系中作出函数y=5的图象,
由题设知,当x=-2或3时,f(x)=5,
且a+1<5即a<4,
由f(-2)=-2×(-2)-1+a=5,
解得a=2;
(2)由|x+1|+|x-a|≥|(x+1)-(x-a)|,
则f(x)min=|a+1|,不等式f(x)≥6恒成立即为
|a+1|≥6,
解得a≤-7或a≥5.
 解:(1)f(x)=|x+1|+|x-a|=
解:(1)f(x)=|x+1|+|x-a|=
|
函数f(x)如图所示.
由题设知:|x+1|+|x-a|≥5解集为(-∞,-2]∪[3,+∞).
如图,在同一坐标系中作出函数y=5的图象,
由题设知,当x=-2或3时,f(x)=5,
且a+1<5即a<4,
由f(-2)=-2×(-2)-1+a=5,
解得a=2;
(2)由|x+1|+|x-a|≥|(x+1)-(x-a)|,
则f(x)min=|a+1|,不等式f(x)≥6恒成立即为
|a+1|≥6,
解得a≤-7或a≥5.
点评:本题考查绝对值不等式的解法,不等式恒成立问题,函数图象的特征,体现了数形结合的数学思想,画出函数f(x)的图象,是解题的关键.

练习册系列答案
相关题目
集合A={1,2,3},集合B={-1,1,3},集合S=A∩B,则集合S的子集有( )
| A、2个 |
| B、3 个 |
| C、4 个 |
| D、8个 |
不等式2x2+3mx+2m>0的解集是R,则m的取值范围是( )
A、m<
| ||
| B、m>0 | ||
C、0<m<
| ||
D、0≤m≤
|
指数函数y=ax的图象经过点(1,2)则a的值是( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |