题目内容
集合A={1，2，3}，集合B={-1，1，3}，集合S=A∩B，则集合S的子集有（ ）
| A、2个 |
| B、3 个 |
| C、4 个 |
| D、8个 |
考点：交集及其运算
专题：集合
分析：根据集合的基本运算进行求解．
解答：
解：∵集合A={1，2，3}，集合B={-1，1，3}，
∴集合S=A∩B={1，3}，
则集合S的子集有22=4个，
故选：C．
∴集合S=A∩B={1，3}，
则集合S的子集有22=4个，
故选：C．
点评：本题主要考查集合的基本运算和集合子集个数的求解，要求熟练掌握集合的交并补运算，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列一定是指数函数的是（ ）
| A、形如y=ax的函数 |
| B、y=xa（a＞0，a≠1） |
| C、y=（|a|+2）-x |
| D、y=（a-2）ax |
已知集合A={0，1，2，3}，集合B={x∈N||x|≤2}，则A∩B=（ ）
| A、{3} |
| B、{1，2} |
| C、{0，1，2} |
| D、{0，1，2，3} |
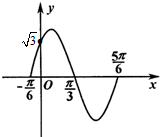函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜