题目内容
已知将圆x2+y2=8上的每一点的纵坐标压缩到原来的
,对应的横坐标不变,得到曲线C;经过点M(2,1)且平行于OM的直线l在y轴上的截距为m(m≠0),直线l与曲线C交于A、B两个不同点.
(1)求曲线C的方程;
(2)求m的取值范围.
| 1 |
| 2 |
(1)求曲线C的方程;
(2)求m的取值范围.
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)在曲线C上任取一个动点P(x,y),根据图象的变换可知点(x,2y)在圆x2+y2=8上.代入圆方程即可求得x和y的关系式,即曲线C的方程.
(2)根据题意可得直线l的方程,进而与椭圆方程联立,消去y,进而根据判别式大于0求得m的范围,进而根据m≠0,最后综合可得答案.
(2)根据题意可得直线l的方程,进而与椭圆方程联立,消去y,进而根据判别式大于0求得m的范围,进而根据m≠0,最后综合可得答案.
解答:
解:(1)在曲线C上任取一个动点P(x,y),
则点(x,2y)在圆x2+y2=8上.…(3分)
所以有x2+(2y)2=8.整理得曲线C的方程为
+
=1.…(6分)
(2)∵直线l平行于OM,且在y轴上的截距为m,又KOM=
,
∴直线l的方程为y=
x+m.…(9分)
由
,得 x2+2mx+2m2-4=0…(10分)
∵直线l与椭圆交于A、B两个不同点,
∴△=(2m)2-4(2m2-4)>0,…(12分)
解得-2<m<2且m≠0.
∴m的取值范围是-2<m<0或0<m<2.…(13分)
则点(x,2y)在圆x2+y2=8上.…(3分)
所以有x2+(2y)2=8.整理得曲线C的方程为
| x2 |
| 8 |
| y2 |
| 2 |
(2)∵直线l平行于OM,且在y轴上的截距为m,又KOM=
| 1 |
| 2 |
∴直线l的方程为y=
| 1 |
| 2 |
由
|
∵直线l与椭圆交于A、B两个不同点,
∴△=(2m)2-4(2m2-4)>0,…(12分)
解得-2<m<2且m≠0.
∴m的取值范围是-2<m<0或0<m<2.…(13分)
点评:本题主要考查了椭圆的标准方程,直线与椭圆的关系.考查了学生分析问题的能力及数学化归思想.

练习册系列答案
相关题目
若原点在圆(x-1)2+(y+2)2=m的内部,则实数m的取值范围是( )
| A、m>5 | B、m<5 |
| C、-2<m<2 | D、0<m<2 |
不等式|2x-log2x|<2x+|log2x|的解集为( )
| A、(1,2) |
| B、(0,1) |
| C、(1,+∞) |
| D、(2,+∞) |
已知x,y,z为非零实数,代数式
+
+
+
的值所组成的集合是M,则下列判断正确的是( )
| x |
| |x| |
| y |
| |y| |
| z |
| |z| |
| |xyz| |
| xyz |
| A、4∈M | B、2∈M |
| C、0∉M | D、-4∉M |
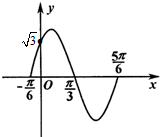 函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<
函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<