题目内容
解方程组
.
|
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:对k分类讨论,利用“消元法”即可得出.
解答:
解:
,
①×k+②可得(k2-1)x=k2+k,
当k≠±1时,x=
,代入①可得y=
-k+1=
.即
.
当k=1时,方程组化为:
,方程组无解;
当k=-1时,方程组化为:x+y=2,方程组有无穷多组解.
综上可得:当k≠±1时,方程组的解为
.
当k=1时,方程组无解;
当k=-1时,方程组有无穷多组解,满足x+y=2.
|
①×k+②可得(k2-1)x=k2+k,
当k≠±1时,x=
| k |
| k-1 |
| k2 |
| k-1 |
| 2k-1 |
| k-1 |
|
当k=1时,方程组化为:
|
当k=-1时,方程组化为:x+y=2,方程组有无穷多组解.
综上可得:当k≠±1时,方程组的解为
|
当k=1时,方程组无解;
当k=-1时,方程组有无穷多组解,满足x+y=2.
点评:本题考查了分类讨论、“消元法”解方程组,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
下列一定是指数函数的是( )
| A、形如y=ax的函数 |
| B、y=xa(a>0,a≠1) |
| C、y=(|a|+2)-x |
| D、y=(a-2)ax |
若原点在圆(x-1)2+(y+2)2=m的内部,则实数m的取值范围是( )
| A、m>5 | B、m<5 |
| C、-2<m<2 | D、0<m<2 |
不等式|2x-log2x|<2x+|log2x|的解集为( )
| A、(1,2) |
| B、(0,1) |
| C、(1,+∞) |
| D、(2,+∞) |
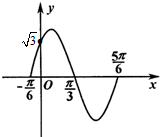 函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<
函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<