题目内容
已知数列{an}的前n项和Sn=n2+2n+1(n∈N*),则an= .
考点:数列的函数特性
专题:等差数列与等比数列
分析:由数列{an}的前n项和Sn求出an=Sn-Sn-1,验证n=1时a1是否满足an即可.
解答:
解:∵数列{an}的前n项和为Sn=n2+2n+1(n∈N*),
∴当n≥2时,Sn-1=(n-1)2+2(n-1)+1,
∴an=Sn-Sn-1
=(n2+2n+1)-[(n-1)2+2(n-1)+1]
=2n+1;
当n=1时,a1=S1=4;
∴an=
.
故答案为:
.
∴当n≥2时,Sn-1=(n-1)2+2(n-1)+1,
∴an=Sn-Sn-1
=(n2+2n+1)-[(n-1)2+2(n-1)+1]
=2n+1;
当n=1时,a1=S1=4;
∴an=
|
故答案为:
|
点评:本题考查了由数列的前n项和公式求通项公式的问题,解题时应用an=Sn-Sn-1求出,是基础题.

练习册系列答案
相关题目
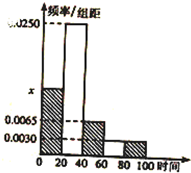 某公司对夏季室外工作人员规定如下:当气温超过35℃时,室外连续工作时间严禁超过100分钟;不少于60分钟的,公司给予适当补助.随机抽取部分工人调查其高温室外连续工作时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中工作时间范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某公司对夏季室外工作人员规定如下:当气温超过35℃时,室外连续工作时间严禁超过100分钟;不少于60分钟的,公司给予适当补助.随机抽取部分工人调查其高温室外连续工作时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中工作时间范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].