题目内容

已知某圆拱桥的水面跨度为20m，拱高为4m，现有一船，船宽为10m，水面以上高为3m，问这条船能否从桥下通过？
考点：抛物线的应用
专题：计算题,圆锥曲线的定义、性质与方程
分析：建立平面直角坐标系，设拱桥型抛物线方程为x2=-2py（p＞0），将B（10，-4）代入，求得抛物线方程，求出A的纵坐标，即可求得结论．
解答： 解：建立平面直角坐标系，设拱桥型抛物线方程为x2=-2py（p＞0）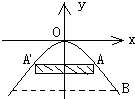
将B（10，-4）代入得2p=25，∴x2=-25y，
当船两侧与抛物线接触时不能通过，
设点A（5，yA），由52=-25yA，得yA=-1，
由于3＞1，故这条船能从桥下通过．
点评：本题考查抛物线的应用，是中档题．解题时要认真审题，恰当地建立坐标系，合理地进行等价转化．
练习册系列答案
相关题目
分别写出函数y=1-2x和函数y=-x2+2x的单调区间．
设函数f（x）=（x-1）2+blnx，其中b为常数．
（1）档b＞
1
2
时，判断函数f（x）在定义域上的单调性；
（2）当b＜
1
2
时，求函数f（x）的极值点．
已知数列{an}的前n项和Sn=n2+2n+1（n∈N*），则an=
 
．
已知椭圆C的两个焦点为F1（-3，0），F2（3，0），点M是椭圆C上的动点，且MF1?MF2的最大值为25．
（1）求椭圆C的方程；
（2）已知有一定点N（2，0），求MN的最小值．
已知函数f（x）=
1
(1-x)2
+2ln（x-1），求函数f（x）的极值．
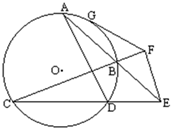延长图O的两弦AB，CD交于圆外一点E，过E点作DA的平行线交CB的廷长线于点F，自F点作图0的切线FG．求证FG=FE．
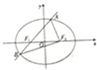如图，椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F1，右焦点为F2，离心率为
3
2
，过F1的直线交椭圆于A，B两点，△ABF2的周长为8．
（1）求椭圆E的方程；
（2）设动直线l：y=kx+m与椭圆E有且只有一个公共点P，且与椭圆E的右准线交于点Q，问在x轴上是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出M的坐标，若不存在，说明理由．
考察下列四个命题，在A处都缺少同一个条件，补上这个条件使其构成真命题（其中l，m为不同的直线，α、β为不重合的平面），则此条件为
 
．
l∥m
m?α
A
⇒l∥α；
l∥m
m∥α
A
⇒l∥α；
l⊥β
α⊥β
A
⇒l∥α；
m⊥α
m⊥l
A
⇒l∥α．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网