题目内容
已知函数f(x)=ax2+(2-a)x-lnx.
(1)当a>0时,求函数f(x)的单调区间;
(2)设a>1,若f(x)在区间[
,1]内的最大值为ln3,求a的值.
(1)当a>0时,求函数f(x)的单调区间;
(2)设a>1,若f(x)在区间[
| 1 |
| a |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:(1)求导且令导数为0,从而求出单调区间的端点,从而确定单调区间.
(2)讨论最值的取得情况,求出a的值.
(2)讨论最值的取得情况,求出a的值.
解答:
解:(1)当a>0时,令f′(x)=0,即2ax2+(2-a)x-1=0.
解得,x=-
<0,x=
>0
则函数f(x)的单调减区间是(0,
),单调增区间是(
,+∞).
(2)由(1)知,
函数f(x)没有极大值点,
∴其最大值要在端点处取得,
而f(1)=2,f(
)=
-1+lna有唯一的极小值ln3,
则a=3.
解得,x=-
| 1 |
| a |
| 1 |
| 2 |
则函数f(x)的单调减区间是(0,
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知,
函数f(x)没有极大值点,
∴其最大值要在端点处取得,
而f(1)=2,f(
| 1 |
| a |
| 3 |
| a |
则a=3.
点评:本题考查了导数的综合应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
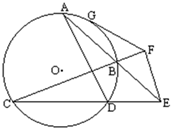 延长图O的两弦AB,CD交于圆外一点E,过E点作DA的平行线交CB的廷长线于点F,自F点作图0的切线FG.求证FG=FE.
延长图O的两弦AB,CD交于圆外一点E,过E点作DA的平行线交CB的廷长线于点F,自F点作图0的切线FG.求证FG=FE.