题目内容
在直角坐标系xOy中,圆C1的参数方程为
(α为参数),圆C2的参数方程为
(β为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(Ⅰ)求C1和C2的极坐标方程;
(Ⅱ)C1和C2交于O,P两点,求P点的一个极坐标.
|
|
(Ⅰ)求C1和C2的极坐标方程;
(Ⅱ)C1和C2交于O,P两点,求P点的一个极坐标.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(I)先把参数方程化为普通方程,再利用
即可得到极坐标方程.
(II)设P(ρ,θ),由8cosθ=4sinθ,解得θ即可得出.
|
(II)设P(ρ,θ),由8cosθ=4sinθ,解得θ即可得出.
解答:
解:( I)圆C1的参数方程为
(α为参数),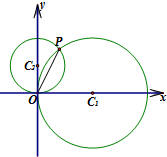
化为普通方程:(x-4)2+y=16,把
代入可得极坐标方程:
ρ=8cosθ.
圆C2的参数方程为
(β为参数),化为普通方程:
x2+(y-2)2=4,可得极坐标方程为ρ=4sinθ.
( II)设P(ρ,θ),则有8cosθ=4sinθ,解得tanθ=2,sinθ=
,
∴P点的极坐标为(
,arcsin
).
|

化为普通方程:(x-4)2+y=16,把
|
ρ=8cosθ.
圆C2的参数方程为
|
x2+(y-2)2=4,可得极坐标方程为ρ=4sinθ.
( II)设P(ρ,θ),则有8cosθ=4sinθ,解得tanθ=2,sinθ=
2
| ||
| 5 |
∴P点的极坐标为(
8
| ||
| 5 |
2
| ||
| 5 |
点评:本题考查了参数方程化为普通方程、化为极坐标方程、两圆的交点,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
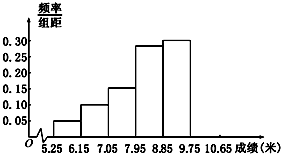 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.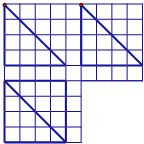 如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为
如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为