题目内容
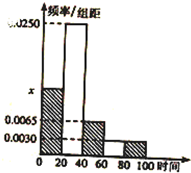 某公司对夏季室外工作人员规定如下:当气温超过35℃时,室外连续工作时间严禁超过100分钟;不少于60分钟的,公司给予适当补助.随机抽取部分工人调查其高温室外连续工作时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中工作时间范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某公司对夏季室外工作人员规定如下:当气温超过35℃时,室外连续工作时间严禁超过100分钟;不少于60分钟的,公司给予适当补助.随机抽取部分工人调查其高温室外连续工作时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中工作时间范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].(1)求频率分布直方图中x的值;
(2)根据频率分布直方图估计样本数据的中位数;
(3)用这个样本的频率分布估计总体分布,将频率视为概率;用分层抽样的方法从享受补助人员和不享受补助人员中抽取25人的样本,检测他们健康状况的变化,那么这两种人员应该各抽取多少人?
考点:频率分布直方图
专题:概率与统计
分析:(1)由频率分布直方图中,各组的累积频率为1,构造关于x的方程,解方程可得答案;
(2)设中位数为t,则20×0.0125+(t-20)×0.0250=0.5,解得中位数;
(3)根据已知数据可得享受补助人员占总体的12%,享受补助人员占总体的88%,进而根据抽取的样本容量为25,得到结论.
(2)设中位数为t,则20×0.0125+(t-20)×0.0250=0.5,解得中位数;
(3)根据已知数据可得享受补助人员占总体的12%,享受补助人员占总体的88%,进而根据抽取的样本容量为25,得到结论.
解答:
解:(1)由直方图可得:20×(x+0.0250+0.0065+0.0030+0.0030)=1,
解得x=0.0125.…(4分)
(2)设中位数为t,则
20×0.0125+(t-20)×0.0250=0.5,得t=30.
样本数据的中位数估计为30分钟.…(8分)
(3)享受补助人员占总体的12%,享受补助人员占总体的88%.
因为共抽取25人,所以应抽取享受补助人员25×12%=3人,
抽取不享受补助人员25×88%=22人.…(12分)
解得x=0.0125.…(4分)
(2)设中位数为t,则
20×0.0125+(t-20)×0.0250=0.5,得t=30.
样本数据的中位数估计为30分钟.…(8分)
(3)享受补助人员占总体的12%,享受补助人员占总体的88%.
因为共抽取25人,所以应抽取享受补助人员25×12%=3人,
抽取不享受补助人员25×88%=22人.…(12分)
点评:本题考查的知识点是频率分布直方图,用样本估计总体,是统计基本概念的直接考查,难度不大,属于基础题.

练习册系列答案
相关题目
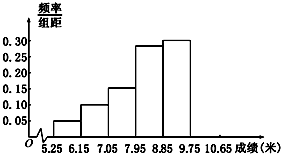 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7. 如图,椭圆E:
如图,椭圆E: