题目内容
求出下列函数的值域:
①y=
;
②y=
;
③y=
.
①y=
| 1 |
| x2-2x+3 |
②y=
| 1 |
| x2-2x-3 |
③y=
| x2 |
| x2+2x+3 |
考点:函数的值域
专题:计算题,函数的性质及应用
分析:依次求函数的值域,注意讨论.①配方法;②配方法;③转化为方程的思想.
解答:
解:①∵
=
,
∴0<
≤
,
故函数的值域为(0,
];
②∵
=
,
又∵(x-1)2-4≥-4,
∴
≤-
或
>0,
∴函数的值域为(-∞,-
]∪(0,+∞);
③∵y=
,且x2+2x+3>0
上式可化为(y-1)x2+2yx+3y=0,
当y-1=0时,方程有解,
当y-1≠0时,△=(2y)2-4(y-1)3y≥0,
解得,0≤y≤
.
综上所述,函数的值域为[0,
].
| 1 |
| x2-2x+3 |
| 1 |
| (x-1)2+2 |
∴0<
| 1 |
| (x-1)2+2 |
| 1 |
| 2 |
故函数的值域为(0,
| 1 |
| 2 |
②∵
| 1 |
| x2-2x-3 |
| 1 |
| (x-1)2-4 |
又∵(x-1)2-4≥-4,
∴
| 1 |
| (x-1)2-4 |
| 1 |
| 4 |
| 1 |
| (x-1)2-4 |
∴函数的值域为(-∞,-
| 1 |
| 4 |
③∵y=
| x2 |
| x2+2x+3 |
上式可化为(y-1)x2+2yx+3y=0,
当y-1=0时,方程有解,
当y-1≠0时,△=(2y)2-4(y-1)3y≥0,
解得,0≤y≤
| 3 |
| 2 |
综上所述,函数的值域为[0,
| 3 |
| 2 |
点评:本题考查了求值域的方法,要注意它们之间的不同.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
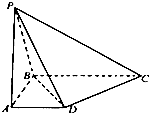 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=1,BC=2,又PB=1,∠PBC=120°,AB⊥PC,直线AB与直线PD所成的角为60°.