题目内容
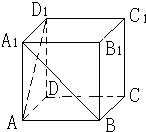
 如图所示,正方体ABCD-A1B1C1D1的棱长为1,点M、N分别是面对角线A1B和B1D1的中点.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,点M、N分别是面对角线A1B和B1D1的中点.(1)求证:MN⊥AB;
(2)求三棱锥N-MBC的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能证明MN⊥AB.
(2)求出平面A1BCD1的一个法向量,从而得到N到平面A1BCD1的距离,由此能求出三棱锥N-MBC的体积.
(2)求出平面A1BCD1的一个法向量,从而得到N到平面A1BCD1的距离,由此能求出三棱锥N-MBC的体积.
解答:
(1)证明:以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
则M(1,
,
),N(
,
,1),
=(-
,0,
),
=(0,1,0),
∵
•
=0,∴MN⊥AB.
(2)设平面A1BCD1的一个法向量
=(x,y,z),
=(0,1,-1),
=(-1,0,0),
由
•
=0,
•
=0,得
,
取y=1,得
=(0,1,1),
点N到平面A1BCD1的距离d=
=
.
S△MBC=
•BC•MB=
,
∴VN-MBC=
S△MBC•d=
×
×
=
.
建立空间直角坐标系,

则M(1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
∵
| AB |
| MN |
(2)设平面A1BCD1的一个法向量
| n |
| A1B |
| BC |
由
| A1B |
| n |
| BC |
| n |
|
取y=1,得
| n |
点N到平面A1BCD1的距离d=
|
| ||||
|
|
| ||
| 4 |
S△MBC=
| 1 |
| 2 |
| ||
| 4 |
∴VN-MBC=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 24 |
点评:本题考查异面直线垂直的证明,考查三棱锥N-MBC的体积的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从10名女学生中选2名,40名男生中选3名,担任五种不同的职务,规定女生不担任其中某种职务,不同的分配方案有( )
| A、A102A403 |
| B、C102A31A44C403 |
| C、C152C403A55 |
| D、C102C403 |
 已知数列{an}的通项公式为an=2n(n∈N*),现将该数列{an}的各项排列成如图的三角数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )
已知数列{an}的通项公式为an=2n(n∈N*),现将该数列{an}的各项排列成如图的三角数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )| A、M(46,16) |
| B、M(46,25) |
| C、M(45,15) |
| D、M(45,25) |
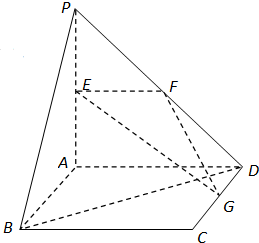 如图,直线PA⊥平面ABCD,四边形ABCD是正方形,且PA=AD=2,点E、F、G分别是线段PA、PD、CD的中点.
如图,直线PA⊥平面ABCD,四边形ABCD是正方形,且PA=AD=2,点E、F、G分别是线段PA、PD、CD的中点.