Question

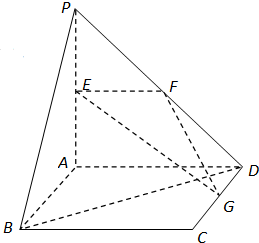如图，直线PA⊥平面ABCD，四边形ABCD是正方形，且PA=AD=2，点E、F、G分别是线段PA、PD、CD的中点．
（1）求异面直线EG与BD所成角的大小（结果用反三角表示）；
（2）在线段CD上是否存在一点Q，使BF⊥EQ，若存在，求出DQ的长，若不存在，请说明理由．

Answer 1

考点：异面直线及其所成的角,直线与平面垂直的性质

专题：空间角

分析：（1）以A为原点建立如图坐标系，求出E，G，B，D，

EG

=(1，2，-1)，

BD

=(-2，2，0)利用数量积求解即可．
（2）假设CD存在点Q，使BF⊥EQ，设DQ=x，则Q（x，2，0），F（0，1，1），通过向量的数量积是否为0．所判断BF⊥EQ．

解答： [理]
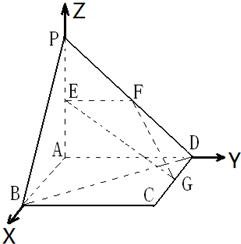
解：（1）以A为原点建立如图坐标系
则E（0，0，1），G（1，2，0），B（2，0，0），D（0，2，0）
因此

EG

=(1，2，-1)，

BD

=(-2，2，0)
所以cosα=|

EG • BD

| EG |•| BD |

|=

2

6 •2 2

=

3

6

．
即异面直线EG与BD所成角的为arccos

3

6

（2）假设CD存在点Q，使BF⊥EQ，设DQ=x，则Q（x，2，0），
F（0，1，1）
因此

BF

=(-2，1，1)，

EQ

=(x，2，-1)
因为BF⊥EQ所以

BF

•

EQ

=0
即DQ=x=

1

2

，
所以CD存在点Q，使BF⊥EQ．

点评：本题考查向量法求解异面直线所成角以及直线的垂直的判断，考查转化思想以及计算能力．