题目内容

已知单位向量
e1
，
e2
的夹角为120°，则|2
e1
-
e2
|=
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量模的平方等于向量的平方解答．
解答： 解：因为单位向量
e1
，
e2
的夹角为120°，所以
e1
•
e2
=1×1×cos120°=-
1
2
，
所以|2
e1
-
e2
|2=4
e1
2+
e2
2-4
e1
e2
=4+1+2=7；
所以|2
e1
-
e2
|=
7
；
故答案为：
7
．
点评：本题考查了向量的数量积以及向量模的运算，属于基础题．
练习册系列答案
相关题目
下列函数中，在定义域内是减函数的为（　　）
A、y=-3x2
B、y=-
1
x
C、y=5x
D、y=-4x
若sinα=2cosα，则
.
cosαsinα
sinαcosα
.
=
 
．
已知命题P：x≤a或x≥3a，q：x≤-2或x≥3，且p是q的充分不必要条件，求a的取值范围．
已知定义在R上的函数f（x）=
1
3
x3+
1
2
（a-4）x2+2（2-a）x+a的图象与y轴的交点和原点的距离小于或等于1．
（1）求实数a的取值范围；
（2）是否存在这样的区间，对任意的a的可能取值，函数f（x）在该区间上都是单调递增的？若存在，则求出这样的区间，若不存在，则说明理由．
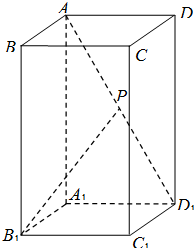如图，已知ABCD-A1B1C1D1是底面为正方形的长方体，∠AD1A1=60°，AD1=4，点P是AD1的中点，求异面直线AA1与B1P所成的角（结果用反三角函数表示）．
求圆心在抛物线x2=4y上，且与直线x+2y+1=0相切的面积最小的圆的方程
 
．
已知椭圆的方程为
x2
9
+
y2
4
=1，点E（1，1），椭圆上是否存在两个不重合的两点M，N，使
OE
=
1
2
（
OM
+
ON
）（O是坐标原点），若存在，求出直线MN的方程，若不存在，请说明理由．
如图所示，正方体ABCD-A1B1C1D1的棱长为1，点M、N分别是面对角线A1B和B1D1的中点．
（1）求证：MN⊥AB；
（2）求三棱锥N-MBC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网