题目内容
11.椭圆x2+8y2=1的短轴端点坐标是( )| A. | (-2$\sqrt{2}$,0),(2$\sqrt{2}$,0) | B. | (-1,0),(1,0) | C. | (0,-$\frac{\sqrt{2}}{4}$),(0,$\frac{\sqrt{2}}{4}$) | D. | $(0,-2\sqrt{2}),(0,2\sqrt{2})$ |
分析 化椭圆方程为标准方程,求得b即可得答案.
解答 解:由椭圆x2+8y2=1,得${x}^{2}+\frac{{y}^{2}}{\frac{1}{8}}=1$.
∴${b}^{2}=\frac{1}{8}$,得b=$\frac{\sqrt{2}}{4}$.
则椭圆短轴端点得坐标为(0,-$\frac{\sqrt{2}}{4}$),(0,$\frac{\sqrt{2}}{4}$).
故选:C.
点评 本题考查椭圆的标准方程,考查椭圆的简单性质,是基础题.

练习册系列答案
相关题目
2.已知$\overrightarrow a=(1\;,\;3)$,$\overrightarrow b=(-2\;,\;5)$,则$3\overrightarrow a-2\overrightarrow b$=( )
| A. | (2,7) | B. | (13,-7) | C. | (7,-1) | D. | (-1,-1) |
19.为了得到函数$y=3sin(x+\frac{π}{3})$的图象,只需将函数y=3sin(x-$\frac{π}{3}$)的图象( )
| A. | 向右平移$\frac{π}{3}$个单位长度 | B. | 向左平移$\frac{π}{3}$个单位长度 | ||
| C. | 向右平移$\frac{2π}{3}$个单位长度 | D. | 向左平移$\frac{2π}{3}$个单位长度 |
20.佳佳同学在8次测试中,数学成绩的茎叶图如图,则这8次成绩的中位数是( )
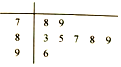

| A. | 86 | B. | 87 | C. | 87.5 | D. | 88.5 |
1.复数$\frac{2}{1-i}$=( )
| A. | $\sqrt{2}$+$\sqrt{2}$i | B. | $\frac{{\sqrt{2}}}{2}$+$\frac{{\sqrt{2}}}{2}$i | C. | 1-i | D. | 1+i |
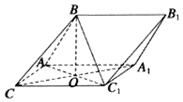 如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.
如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.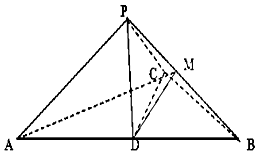 如图,在三棱锥P-ABC中,∠ACB=90°,CB=4,AB=12,D为
如图,在三棱锥P-ABC中,∠ACB=90°,CB=4,AB=12,D为