题目内容
2.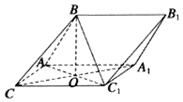 如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.
如图,三棱柱ABC-A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.(Ⅰ)求证:BO⊥平面AA1C1C;
(Ⅱ)求二面角A-BC1-B1的余弦值.
分析 (Ⅰ)推导出BO⊥AC1,由此利用平面ABC1⊥平面AA1C1C,能证明BO⊥平面AA1C1C.
(Ⅱ)以O为坐标原点,建空间直角坐标系,利用向量法能求出二面角的余弦值.
解答 证明:(Ⅰ)依题意,四边形AA1C1C为菱形,且∠AA1C1=60°
∴△AA1C1为正三角形,又∠BAC1=60°,
∴△BAC1为正三角形,又O为AC1中点,
∴BO⊥AC1,
∵平面ABC1⊥平面AA1C1C,平面ABC1∩平面AA1C1C=AC1,
∵BO?平面AA1CC1,∴BO⊥平面AA1C1C.…(4分)
解:(Ⅱ)以O为坐标原点,建空间直角坐标系,如图,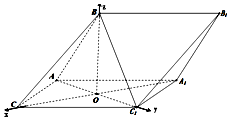
令AB=2,则$A(0,-1,0),C(\sqrt{3},0,0),B(0,0,\sqrt{3})$,C1(0,1,0)
∴$\overrightarrow{B{C_1}}=(0,1,-\sqrt{3})$,$\overrightarrow{B{B_1}}=\overrightarrow{C{C_1}}=(-\sqrt{3},1,0)$
设平面BB1C1的一个法向量为$\overrightarrow{n_1}=(x,y,z)$,
由$\left\{{\begin{array}{l}{\overrightarrow{n_1}•\overrightarrow{B{C_1}}=0}\\{\overrightarrow{n_1}•\overrightarrow{B{B_1}}=0}\end{array}}\right.$得$\left\{{\begin{array}{l}{y-\sqrt{3}z=0}\\{-\sqrt{3}x+y=0}\end{array}}\right.$,
取z=1,得$\overrightarrow{n_1}=(1,\sqrt{3},1)$…(9分)
又面ABC1的一个法向量为$\overrightarrow{n_2}=\overrightarrow{OC}=(\sqrt{3},0,0)$
∴$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}||\overrightarrow{n_2}|}}=\frac{{\sqrt{5}}}{5}$ …(11分)
故所求二面角的余弦值为$-\frac{{\sqrt{5}}}{5}$…(12分)
点评 本题考查线线垂直的证明,考查线面角的正弦值的求法,考查空间中线线、线面、面面间的位置关系,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案| A. | cosα-sinα | B. | sinα+cosα+2 | C. | sinα-cosα | D. | -sinα-cosα-2 |
| A. | 12种 | B. | 16种 | C. | 20种 | D. | 24种 |
| A. | (-2$\sqrt{2}$,0),(2$\sqrt{2}$,0) | B. | (-1,0),(1,0) | C. | (0,-$\frac{\sqrt{2}}{4}$),(0,$\frac{\sqrt{2}}{4}$) | D. | $(0,-2\sqrt{2}),(0,2\sqrt{2})$ |
 如图,四棱锥P-ABCD中,底面ABCD是菱形,$∠BAD=\frac{π}{3}$,PA=PD,F为AD的中点,PD⊥BF.
如图,四棱锥P-ABCD中,底面ABCD是菱形,$∠BAD=\frac{π}{3}$,PA=PD,F为AD的中点,PD⊥BF.